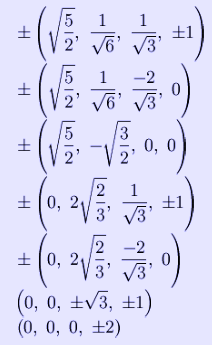In four dimensional geometry, the runcinated pentachoron is a 4-dimensional convex uniform polytope (or uniform polychoron) constructed by expanding the cells of a pentachoron radially and filling in the gaps with triangular prisms (which are the face prisms and edge figures) and tetrahedra (cells of the dual pentachoron). It consists of 10 tetrahedra and 20 triangular prisms. The 10 tetrahedra correspond with the cells of a pentachoron and its dual.

Structure

of the ten tetrahedral cells meet at each vertex. The triangular prisms lie between them, joined to them by their triangular faces and to each other by their square faces. Each triangular prism is joined to its neighbouring triangular prisms in anti orientation (i.e., if edges A and B in the shared square face are joined to the triangular faces of one prism, then it is the other two edges that are joined to the triangular faces of the other prism); thus each pair of adjacent prisms, if rotated into the same hyperplane, would form a gyrobifastigium.

Coordinates

The Cartesian coordinates of the vertices of an origin-centered runcinated pentachoron with edge length 2 are:

An alternate simpler set of coordinates can be made in 5-space, as 20 permutations of:

(0,1,1,1,2)

This construction exists as one of 32 orthant facets of the runcinated pentacross.

Cross-sections

The maximal cross-section of the runcinated 5-cell with a 3-dimensional hyperplane is a cuboctahedron. This cross-section divides the runcinated 5-cell into two tetrahedral hypercupolas consisting of 5 tetrahedra and 10 triangular prisms each.

Projections

The tetrahedron-first orthographic projection of the runcinated pentachoron into 3-dimensional space has a cuboctahedral envelope. The structure of this projection is as follows:

* The cuboctahedral envelope is divided internally as follows:

* Four flattened tetrahedra join 4 of the triangular faces of the cuboctahedron to a central tetrahedron. These are the images of 5 of the tetrahedral cells.
* The 6 square faces of the cuboctahedron are joined to the edges of the central tetrahedron via distorted triangular prisms. These are the images of 6 of the triangular prism cells.
* The other 4 triangular faces are joined to the central tetrahedron via 4 triangular prisms (distorted by projection). These are the images of another 4 of the triangular prism cells.
* This accounts for half of the runcinated 5-cell (5 tetrahedra and 10 triangular prisms), which may be thought of as the 'northern hemisphere'.

* The other half, the 'southern hemisphere', corresponds to an isomorphic division of the cuboctahedron in dual orientation, in which the central tetrahedron is dual to the one in the first half. The triangular faces of the cuboctahedron join the triangular prisms in one hemisphere to the flattened tetrahedra in the other hemisphere, and vice versa. Thus, the southern hemisphere contains another 5 tetrahedra and another 10 triangular prisms, making the total of 10 tetrahedra and 20 triangular prisms.

Images

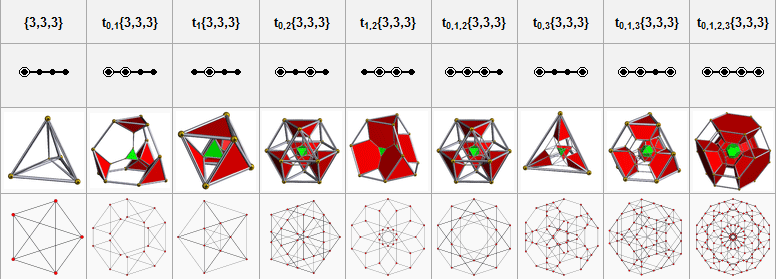
Alternative names

* Runcinated 5-cell (Norman Johnson)
* Runcinated pentachoron
* Runcinated 4-simplex
* Small prismatodecachoron
* Spid (Jonathan Bowers: for small prismatodecachoron)

Related uniform polychora

The runcinated pentachoron is one of 9 uniform polychora constructed from the [3,3,3] Coxeter group.

Name	5-cell	truncated 5-cell	rectified 5-cell	cantellated 5-cell	bitruncated 5-cell	cantitruncated 5-cell	runcinated 5-cell	runcitruncated 5-cell	omnitruncated 5-cell
Schläfli symbol
Coxeter-Dynkin diagram
Schlegel diagram
Coxeter plane projection

Images: Robert Webb's Great Stella software

Geometry