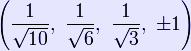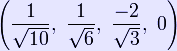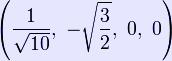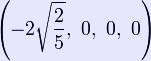Pentachoron

In geometry, the pentachoron is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as the 5-cell, pentatope, or hyperpyramid. It is a 4-simplex, the simplest possible convex regular 4-polytope (four-dimensional analogue of a polyhedron), and is analogous to the tetrahedron in three dimensions and the triangle in two dimensions.

The regular pentachoron is bounded by regular tetrahedra, and is one of the six regular convex polychora, represented by Schläfli symbol {3,3,3}.

Geometry

The pentachoron is self-dual, and its vertex figure is a tetrahedron. Its maximal intersection with 3-dimensional space is the triangular prism. Its dihedral angle is cos−1(1/4), or approximately 75.52°.

Construction

The pentachoron can be constructed from a tetrahedron by adding a 5th vertex such that it is equidistant from all the other vertices of the tetrahedron. (The pentachoron is essentially a 4-dimensional pyramid with a tetrahedral base.)

The Cartesian coordinates of the vertices of an origin-centered regular pentachoron having edge length 2 are:

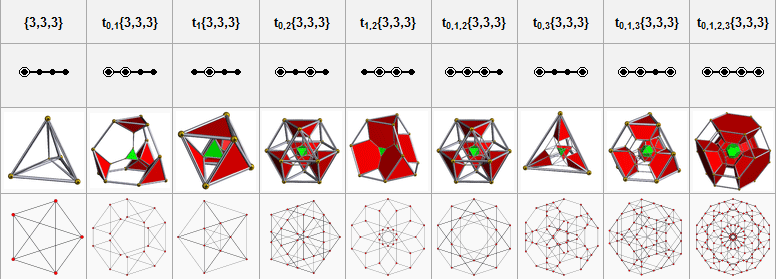
The vertices of a 4-simplex (with edge √2) can be more simply constructed on a hyperplane in 5-space, as permutations of (0,0,0,0,1) or (0,1,1,1,1); in these positions it is a facet of, respectively, the 5-orthoplex or the rectified penteract.

Projections

Alternative names

* 5-cell
* 4-simplex
* Pentatope
* Pentahedroid (Henry Parker Manning)
* Pen (Jonathan Bowers: for pentachoron)
* Hyperpyramid

Related uniform polychora

The pentachoron (5-cell) is the simplest of 9 uniform polychora constructed from the [3,3,3] Coxeter group.

Name	5-cell	truncated 5-cell	rectified 5-cell	cantellated 5-cell	bitruncated 5-cell	cantitruncated 5-cell	runcinated 5-cell	runcitruncated 5-cell	omnitruncated 5-cell
Schläfli symbol
Coxeter-Dynkin diagram
Schlegel diagram
Coxeter plane projection

Images: Robert Webb's Great Stella software

Geometry