In four dimensional geometry, the cantellated 5-cell is a uniform polychoron. It has 30 vertices, 90 edges, 80 faces, and 20 cells. The cells are 5 cuboctahedra, 5 octahedra, and 10 triangular prisms. Each vertex is surrounded by 2 cuboctahedra, 2 triangular prisms, and 1 octahedron; the vertex figure is a nonuniform triangular prism.

Alternate names

* Cantellated pentachoron
* Cantellated 4-simplex
* (small) prismatodispentachoron
* Rectified dispentachoron
* Srip (Jonathan Bowers: for small rhombated pentachoron)

Images

Coordinates

The Cartesian coordinates of the vertices of the origin-centered cantellated 5-cell having edge length 2 are:

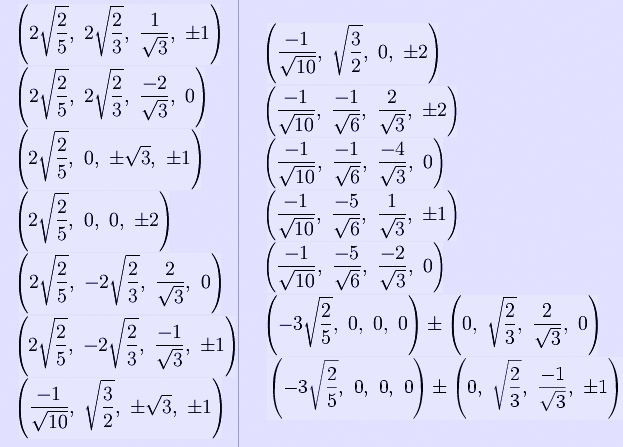
The vertices of the cantellated 5-cell can be most simply positioned in 5-space as permutations of:

(0,0,1,1,2)

Related uniform polychora

The cantellated pentachoron is one of 9 uniform polychora constructed from the [3,3,3] Coxeter group.

Name	5-cell	truncated 5-cell	rectified 5-cell	cantellated 5-cell	bitruncated 5-cell	cantitruncated 5-cell	runcinated 5-cell	runcitruncated 5-cell	omnitruncated 5-cell
Schläfli symbol
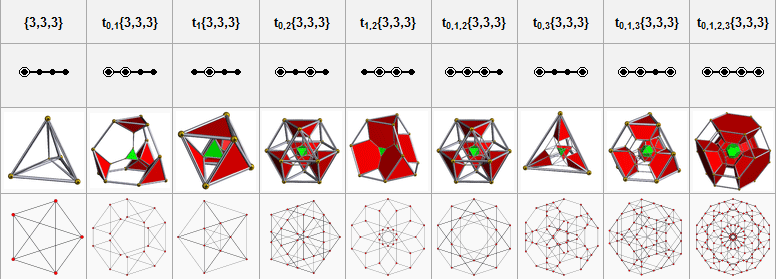Coxeter-Dynkin diagram
Schlegel diagram
Coxeter plane projection

Images: Robert Webb's Great Stella software