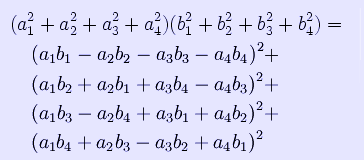Euler's four-square identity

In mathematics, Euler's four-square identity says that the product of two numbers, each of which being a sum of four squares, is itself a sum of four squares. Specifically:

Euler wrote about this identity in the letter CXXV, April 12, 1749, to Goldbach (but note that he used a different sign convention from the above). It can be proven with elementary algebra and holds in every commutative ring. If the as and bs are real numbers, a more elegant proof is available: the identity expresses the fact that the absolute value of the product of two quaternions is equal to the product of their absolute values, in the same way that the Brahmagupta-Fibonacci two-square identity does for complex numbers.

The identity was used by Lagrange to prove his four square theorem. More specifically, it allows the theorem to be proven only for prime numbers.

Lagrange's four-square theorem

See also

* Brahmagupta-Fibonacci identity

* Degen's eight-square identity

Number Theory