Parallelohedron

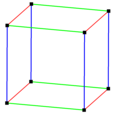
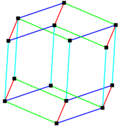
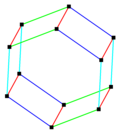
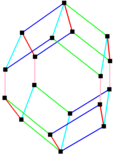
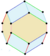
In geometry a parallelohedron is a polyhedron that can tessellate 3-dimensional spaces with face-to-face contacts via translations. This requires all opposite faces be congruent. Parallelohedra can only have parallelogonal faces, either parallelograms or hexagons with parallel opposite edges.

There are 5 types, first identified by Evgraf Fedorov in his studies of crystallographic systems.

Topological types

The vertices of parallelohedra can be computed by linear combinations of 3 to 6 vectors. Each vector can have any length greater than zero, with zero length becoming degenerate, or becoming a smaller parallelohedra.

The greatest parallelohedron is a truncated octahedron which is also called a 4-permutahedron and can be represented with in a 4D in a hyperplane coordinates as all permutations of the counting numbers (1,2,3,4).

A belt mn means n directional vectors, each containing m coparallel congruent edges. Every type has order 2 Ci central inversion symmetry in general, but each has higher symmetry geometries as well.

Name	Cube (parallelepiped)	Rhombic dodecahedron	Hexagonal prism Elongated cube	Elongated dodecahedron	Truncated octahedron
Images
Edge types	3 edge-lengths	4 edge-lengths	3+1 edge-lengths	4+1 edge-lengths	6 edge-lengths
Belts	43	64	43, 61	64, 41	66

Symmetries of 5 types

There are 5 types of parallelohedra, although each has forms of varied symmetry.

#	Polyhedron	Symmetry (order)	Image	Vertices	Edges	Faces	Belts
1	Rhombohedron	Ci (2)		8	12	6	43
	Trigonal trapezohedron	D3d (12)
	Parallelepiped	Ci (2)
	Rectangular cuboid	D2h (8)
	Cube	Oh (24)
2	Hexagonal prism	Ci (2)		8	18	12	61, 43
		D6h (24)
3	Rhombic dodecahedron	D2h (8)		14	24	12	64
		Oh (24)
4	Elongated dodecahedron	D4h (16)		18	28	12	64, 41
		D2h (8)
5	Truncated octahedron	Oh (24)		24	36	14	66

High symmetric examples

Pm3m (221)	Im3m (229)		Fm3m (225)
Cubic	Hexagonal prismatic	Rhombic dodecahedral	Elongated dodecahedral	Bitruncated cubic

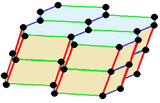
General symmetry examples

See also

parallelogon - analogous space-filling polygons in 2D, with parallelograms and hexagons
parallelotope

References

The facts on file: Geometry handbook, Catherine A. Gorini, 2003, ISBN 0-8160-4875-4, p.117
Coxeter, H. S. M. Regular polytopes (book), 3rd ed. New York: Dover, pp. 29-30, p.257, 1973.
Tutton, A. E. H. Crystallography and Practical Crystal Measurement, 2nd ed. London: Lubrecht & Cramer, 1964.
Weisstein, Eric W., "Primary parallelohedron", MathWorld.
Weisstein, Eric W., "Space-filling polyhedron", MathWorld.
E. S. Fedorov, Nachala Ucheniya o Figurah. [In Russian] (Elements of the theory of figures) Notices Imper. Petersburg Mineralog. Soc., 2nd ser.,24(1885), 1 – 279. Republished by the Acad. Sci. USSR, Moscow 1953.
Fedorov's five parallelohedra in R³
Fedorov's Five Parallelohedra

Mathematics Encyclopedia