Hellenica World

Pentagonal Icositetrahedron

In[260]:=

"PentagonalIcositetrahedron_2.gif"

Out[260]=

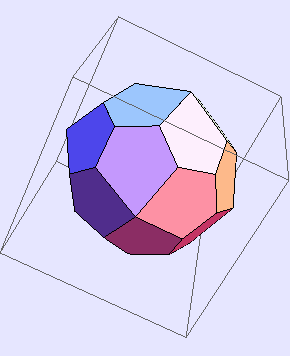
"PentagonalIcositetrahedron_3.gif"

In[261]:=

"PentagonalIcositetrahedron_4.gif"

Out[261]=

"PentagonalIcositetrahedron_5.gif"

In[262]:=

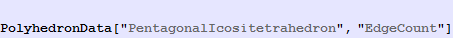
"PentagonalIcositetrahedron_6.gif"

Out[262]=

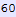
"PentagonalIcositetrahedron_7.gif"

In[263]:=

"PentagonalIcositetrahedron_8.gif"

Out[263]=

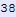
"PentagonalIcositetrahedron_9.gif"

In[264]:=

"PentagonalIcositetrahedron_10.gif"

Out[264]=

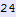
"PentagonalIcositetrahedron_11.gif"

In[265]:=

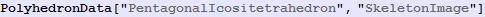
"PentagonalIcositetrahedron_12.gif"

Out[265]=

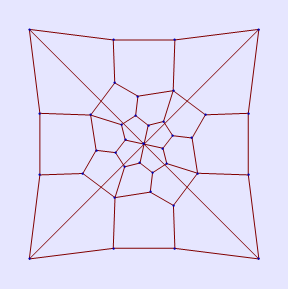
"PentagonalIcositetrahedron_13.gif"

In[266]:=

"PentagonalIcositetrahedron_14.gif"

Out[266]=

"PentagonalIcositetrahedron_15.gif"

In[267]:=

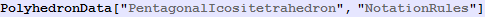
"PentagonalIcositetrahedron_16.gif"

Out[267]=

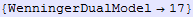
"PentagonalIcositetrahedron_17.gif"

In[268]:=

"PentagonalIcositetrahedron_18.gif"

Out[268]//InputForm=

Graphics3D[GraphicsComplex[{{0, 0, Root[-1 - 4*#1^2 - 336*#1^4 + 64*#1^6 & , 1, 0]}, {0, 0, Root[-1 - 4*#1^2 - 336*#1^4 + 64*#1^6 & , 2, 0]},
   {0, Root[-1 - 4*#1^2 - 336*#1^4 + 64*#1^6 & , 1, 0], 0}, {0, Root[-1 - 4*#1^2 - 336*#1^4 + 64*#1^6 & , 2, 0], 0},
   {Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 1, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 1, 0]}, {Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 2, 0]},
   {Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 1, 0], Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0]}, {Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0]},
   {Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 2, 0]}, {Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 2, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 1, 0]},
   {Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0]}, {Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 2, 0],
    Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0]},
   {Root[-1 - 4*#1^2 - 336*#1^4 + 64*#1^6 & , 1, 0], 0, 0}, {Root[-1 - 4*#1^2 - 336*#1^4 + 64*#1^6 & , 2, 0], 0, 0},
   {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0], Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 2, 0]}, {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0],
    Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 1, 0]},
   {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0]}, {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0]},
   {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0]}, {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0]},
   {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0], Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 1, 0],
    Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 1, 0]}, {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 2, 0], Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 2, 0]},
   {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0], Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 1, 0]}, {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0],
    Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 2, 0]},
   {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0]}, {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0]},
   {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0]}, {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0]},
   {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 1, 0],
    Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 2, 0]}, {Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0],
    Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 2, 0], Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 1, 0]},
   {Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 1, 0], Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0]}, {Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 1, 0],
    Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0]},
   {Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 1, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0],
    Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 2, 0]}, {Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0], Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 1, 0]},
   {Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 2, 0], Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 1, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0]}, {Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 2, 0],
    Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0]},
   {Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 2, 0], Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 1, 0],
    Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 1, 0]}, {Root[-1 + 4*#1^2 + 16*#1^4 + 64*#1^6 & , 2, 0],
    Root[-1 + 20*#1^2 - 112*#1^4 + 64*#1^6 & , 2, 0], Root[-49 + 164*#1^2 - 240*#1^4 + 64*#1^6 & , 2, 0]}},
  Polygon[{{5, 13, 8, 21, 17}, {22, 20, 6, 13, 7}, {15, 18, 7, 13, 5}, {8, 13, 6, 16, 19}, {14, 12, 29, 26, 9}, {11, 30, 27, 10, 14},
    {9, 23, 25, 11, 14}, {14, 10, 24, 28, 12}, {35, 33, 18, 15, 3}, {34, 19, 16, 4, 36}, {31, 17, 21, 1, 37}, {38, 32, 20, 22, 2},
    {3, 31, 37, 25, 23}, {28, 24, 4, 32, 38}, {26, 29, 2, 33, 35}, {1, 34, 36, 27, 30}, {15, 5, 17, 31, 3}, {4, 16, 6, 20, 32},
    {2, 22, 7, 18, 33}, {21, 8, 19, 34, 1}, {9, 26, 35, 3, 23}, {27, 36, 4, 24, 10}, {25, 37, 1, 30, 11}, {12, 28, 38, 2, 29}}]]]

In[269]:=

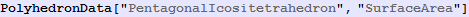
"PentagonalIcositetrahedron_19.gif"

Out[269]=

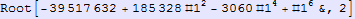
"PentagonalIcositetrahedron_20.gif"

In[270]:=

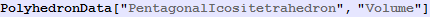
"PentagonalIcositetrahedron_21.gif"

Out[270]=

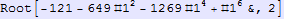
"PentagonalIcositetrahedron_22.gif"

In[271]:=

"PentagonalIcositetrahedron_23.gif"

Out[271]=

"PentagonalIcositetrahedron_24.gif"