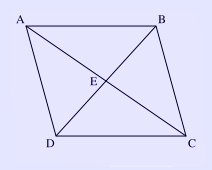
In geometry, a parallelogram is a quadrilateral with two sets of parallel sides. The opposite sides of a parallelogram are of equal length, and the opposite angles of a parallelogram are congruent. The three-dimensional counterpart of a parallelogram is a parallelepiped. The parallelogram must have 2 of the same size acute angles and 2 of the same size obtuse angles.

Properties

* The two parallel sides are of equal length.
* The area, A, of a parallelogram is A = BH, where B is the base of the parallelogram and H is its height.
* The area of a parallelogram is twice the area of a triangle created by one of its diagonals.
* The area is also equal to the magnitude of the vector cross product of two adjacent sides.
* The diagonals of a parallelogram bisect each other.
* It is possible to create a tessellation of a plane with any parallelogram.
* The parallelogram is a special case of the trapezoid.
* The rectangle is a special case of the parallelogram.
* The rhombus is a special case of the parallelogram.

Vector spaces

In a vector space, addition of vectors is usually defined using the parallelogram law. The parallelogram law distinguishes Hilbert spaces from other Banach spaces.

Computing the area of a parallelogram

Let and let denote the matrix with columns a and b. Then the area of the parallelogram generated by a and b is equal to | det(V) |

Let and let . Then the area of the parallelogram generated by a and b is equal to

Proof that diagonals bisect each other

To prove that the diagonals of a parallelogram bisect each other, first note a few pairs of equivalent angles:

Since they are angles that a transversal makes with parallel lines AB and DC.

Also, since they are a pair of vertical angles.

Therefore, since they have the same angles.

From this similarity, we have the ratios

Since AB = DC, we have

.

Therefore,

AE = CE

BE = DE

E bisects the diagonals AC and BD.

See also

* Fundamental parallelogram

* Parallelogram of force

* Rhombus

* Synthetic geometry

* Gnomon (figure)

Links

Geometry