Hellenica World

Metabiaugmented dodecahedron

In[686]:=

"MetabiaugmentedDodecahedron_2.gif"

Out[686]=

"MetabiaugmentedDodecahedron_3.gif"

In[687]:=

"MetabiaugmentedDodecahedron_4.gif"

Out[687]=

"MetabiaugmentedDodecahedron_5.gif"

In[688]:=

"MetabiaugmentedDodecahedron_6.gif"

Out[688]=

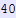
"MetabiaugmentedDodecahedron_7.gif"

In[689]:=

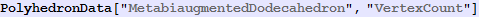
"MetabiaugmentedDodecahedron_8.gif"

Out[689]=

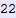
"MetabiaugmentedDodecahedron_9.gif"

In[690]:=

"MetabiaugmentedDodecahedron_10.gif"

Out[690]=

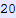
"MetabiaugmentedDodecahedron_11.gif"

In[691]:=

"MetabiaugmentedDodecahedron_12.gif"

Out[691]=

"MetabiaugmentedDodecahedron_13.gif"

In[692]:=

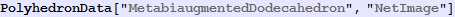
"MetabiaugmentedDodecahedron_14.gif"

Out[692]=

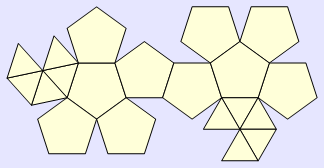
"MetabiaugmentedDodecahedron_15.gif"

In[693]:=

"MetabiaugmentedDodecahedron_16.gif"

Out[693]=

"MetabiaugmentedDodecahedron_17.gif"

In[694]:=

"MetabiaugmentedDodecahedron_18.gif"

Out[694]//InputForm=

Graphics3D[GraphicsComplex[{{1/(8*Sqrt[6*(47 + 21*Sqrt[5])]), (-1 + Sqrt[5])/32,
    -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[9 - 36*#1^2 + 16*#1^4 & , 4, 0]},
   {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]), (-1 + Sqrt[5])/32, -Sqrt[(7 - 3*Sqrt[5])/6]/8 +
     Root[9 - 36*#1^2 + 16*#1^4 & , 1, 0]}, {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) +
     Root[1 - 36*#1^2 + 144*#1^4 & , 3, 0], (-3 - Sqrt[5])/4 + (-1 + Sqrt[5])/32,
    -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[1 - 36*#1^2 + 144*#1^4 & , 4, 0]},
   {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[1 - 36*#1^2 + 144*#1^4 & , 3, 0],
    (-1 + Sqrt[5])/32 + (3 + Sqrt[5])/4, -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[1 - 36*#1^2 + 144*#1^4 & , 4, 0]},
   {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[1 - 36*#1^2 + 144*#1^4 & , 4, 0],
    (-1 - Sqrt[5])/4 + (-1 + Sqrt[5])/32, -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[25 - 180*#1^2 + 144*#1^4 & , 1,
      0]}, {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[1 - 36*#1^2 + 144*#1^4 & , 4, 0],
    (-1 + Sqrt[5])/32 + (1 + Sqrt[5])/4, -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[25 - 180*#1^2 + 144*#1^4 & , 1,
      0]}, {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[25 - 180*#1^2 + 144*#1^4 & , 4, 0],
    (-1 - Sqrt[5])/4 + (-1 + Sqrt[5])/32, -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[1 - 36*#1^2 + 144*#1^4 & , 4,
      0]}, {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[25 - 180*#1^2 + 144*#1^4 & , 4, 0],
    (-1 + Sqrt[5])/32 + (1 + Sqrt[5])/4, -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[1 - 36*#1^2 + 144*#1^4 & , 4, 0]},
   {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[1 - 216*#1^2 + 144*#1^4 & , 1, 0], -1/2 + (-1 + Sqrt[5])/32,
    -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[1 - 36*#1^2 + 144*#1^4 & , 4, 0]},
   {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[1 - 216*#1^2 + 144*#1^4 & , 1, 0], 1/2 + (-1 + Sqrt[5])/32,
    -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[1 - 36*#1^2 + 144*#1^4 & , 4, 0]},
   {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[1 - 216*#1^2 + 144*#1^4 & , 4, 0], -1/2 + (-1 + Sqrt[5])/32,
    -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[1 - 36*#1^2 + 144*#1^4 & , 1, 0]},
   {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[1 - 216*#1^2 + 144*#1^4 & , 4, 0], 1/2 + (-1 + Sqrt[5])/32,
    -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[1 - 36*#1^2 + 144*#1^4 & , 1, 0]},
   {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[1 - 9*#1^2 + 9*#1^4 & , 1, 0], (-1 + Sqrt[5])/32,
    -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[25 - 180*#1^2 + 144*#1^4 & , 1, 0]},
   {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[1 - 36*#1^2 + 144*#1^4 & , 1, 0],
    (-1 - Sqrt[5])/4 + (-1 + Sqrt[5])/32, -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[25 - 180*#1^2 + 144*#1^4 & , 4,
      0]}, {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[1 - 36*#1^2 + 144*#1^4 & , 1, 0],
    (-1 + Sqrt[5])/32 + (1 + Sqrt[5])/4, -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[25 - 180*#1^2 + 144*#1^4 & , 4,
      0]}, {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[1 - 9*#1^2 + 9*#1^4 & , 4, 0], (-1 + Sqrt[5])/32,
    -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[25 - 180*#1^2 + 144*#1^4 & , 4, 0]},
   {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[25 - 180*#1^2 + 144*#1^4 & , 1, 0],
    (-1 - Sqrt[5])/4 + (-1 + Sqrt[5])/32, -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[1 - 36*#1^2 + 144*#1^4 & , 1,
      0]}, {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[25 - 180*#1^2 + 144*#1^4 & , 1, 0],
    (-1 + Sqrt[5])/32 + (1 + Sqrt[5])/4, -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[1 - 36*#1^2 + 144*#1^4 & , 1, 0]},
   {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[121 - 345*#1^2 + 225*#1^4 & , 1, 0], (-1 + Sqrt[5])/32,
    -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[121 - 6180*#1^2 + 3600*#1^4 & , 4, 0]},
   {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[1 - 36*#1^2 + 144*#1^4 & , 2, 0],
    (-3 - Sqrt[5])/4 + (-1 + Sqrt[5])/32, -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[1 - 36*#1^2 + 144*#1^4 & , 1,
      0]}, {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[1 - 36*#1^2 + 144*#1^4 & , 2, 0],
    (-1 + Sqrt[5])/32 + (3 + Sqrt[5])/4, -Sqrt[(7 - 3*Sqrt[5])/6]/8 + Root[1 - 36*#1^2 + 144*#1^4 & , 1, 0]},
   {1/(8*Sqrt[6*(47 + 21*Sqrt[5])]) + Root[121 - 2520*#1^2 + 3600*#1^4 & , 4, 0],
    (-5 - 4*Sqrt[5])/10 + (-1 + Sqrt[5])/32, -Sqrt[(7 - 3*Sqrt[5])/6]/8 +
     Root[121 - 1620*#1^2 + 3600*#1^4 & , 2, 0]}},
  Polygon[{{2, 6, 12, 11, 5}, {11, 12, 8, 16, 7}, {12, 6, 21, 4, 8}, {6, 2, 13, 18, 21}, {2, 5, 20, 17, 13},
    {4, 21, 18, 10, 15}, {18, 13, 17, 9, 10}, {17, 20, 3, 14, 9}, {3, 7, 16, 1, 14}, {16, 8, 4, 15, 1},
    {19, 15, 10}, {19, 10, 9}, {19, 9, 14}, {19, 14, 1}, {19, 1, 15}, {22, 5, 11}, {22, 11, 7}, {22, 7, 3},
    {22, 3, 20}, {22, 20, 5}}]]]

In[695]:=

"MetabiaugmentedDodecahedron_19.gif"

Out[695]=

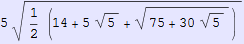
"MetabiaugmentedDodecahedron_20.gif"

In[696]:=

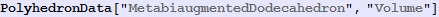
"MetabiaugmentedDodecahedron_21.gif"

Out[696]=

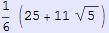
"MetabiaugmentedDodecahedron_22.gif"

In[697]:=

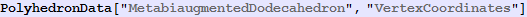
"MetabiaugmentedDodecahedron_23.gif"

Out[697]=

"MetabiaugmentedDodecahedron_24.gif"

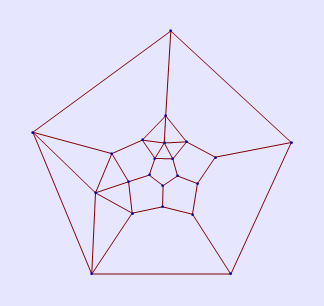
Johnson Polyhedra

Geometry