Salt bridge (protein and supramolecular)

In chemistry, a salt bridge is a combination of two noncovalent interactions: hydrogen bonding and electrostatic interactions (Figure 1). This is most commonly observed to contribute stability to the entropically unfavorable folded conformation of proteins. Although noncovalent interactions are known to be relatively weak interactions, small stabilizing interactions can add up to make an important contribution to the overall stability of a conformer.[1] Not only are salt bridges found in proteins, but they can also be found in supramolecular chemistry. The thermodynamics of each are explored through experimental procedures to assess the free energy contribution of the salt bridge to the overall free energy of the state.

Figure 1. Example of salt bridge between amino acids glutamic acid and lysine demonstrating electrostatic interaction and hydrogen bonding

Salt bridges found in proteins

Figure 2. Wild type (left) and mutated (right) form of lamin A (LMNA, PDB: 1IFR). Normally, arginine 527 (blue) forms salt bridge with glutamate 537 (magenta), but R527L mutation causes loss of the complementary negative charge and structure destabilization. At the phenotype level this manifests with overlapping mandibuloacral dysplasia and progeria syndrome.[2]

The salt bridge most often arises from the anionic carboxylate (RCOO−) of either aspartic acid or glutamic acid and the cationic ammonium (RNH3+) from lysine or the guanidinium (RNHC(NH2)2+) of arginine (Figure 2).[1] Although these are the most common, other residues with ionizable side chains such as histidine, tyrosine, and serine can also participate, depending on outside factors perturbing their pKa's. The distance between the residues participating in the salt bridge is also cited as being important. The distance required is less than 4 Å (400 pm). Amino acids greater than this distance apart do not qualify as forming a salt bridge.[3] Due to the numerous ionizable side chains of amino acids found throughout a protein, the pH at which a protein is placed is crucial to its stability.

Methods for quantifying salt bridge stability

Figure 3. A salt bridge in T4 lysozyme between aspartic acid (Asp) at residue 70 and a histidine (His) at residue 31

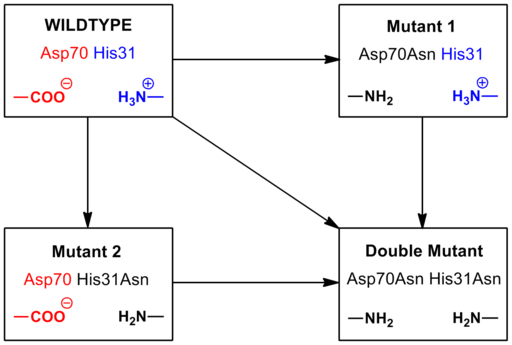
The contribution of a salt bridge to the overall stability to the folded state of a protein can be assessed through thermodynamic data gathered from mutagenesis studies and nuclear magnetic resonance techniques.[4] Using a mutated pseudo-wild-type protein specifically mutated to prevent precipitation at high pH, the salt bridge’s contribution to the overall free energy of the folded protein state can be determined by performing a point-mutation, altering and, consequently, breaking the salt bridge. For example, a salt bridge was identified to exist in the T4 lysozyme between aspartic acid (Asp) at residue 70 and a histidine (His) at residue 31 (Figure 3). Site-directed mutagenesis with asparagine (Asn) (Figure 4) was done obtaining three new mutants: Asp70Asn His31 (Mutant 1), Asp70 His31Asn (Mutant 2), and Asp70Asn His31Asn (Double Mutant).

Figure 4. Mutagenesis of T4 lysozyme salt bridge between Asp 70 and His 31

Once the mutants have been established, two methods can be employed to calculate the free energy associated with a salt bridge. One method involves the observation of the melting temperature of the wild-type protein versus that of the three mutants. The denaturation can be monitored through a change in circular dichroism. A reduction in melting temperature indicates a reduction in stability. This is quantified through a method described by Becktel and Schellman where the free energy difference between the two is calculated through ΔTΔS.[5] There are some issues with this calculation and can only be used with very accurate data. In the T4 lysozyme example, ΔS of the pseudo-wild-type had previously been reported at pH 5.5 so the midpoint temperature difference of 11 °C at this pH multiplied by the reported ΔS of 360 cal/(mol·K) (1.5 kJ/(mol·K)) yields a free energy change of about −4 kcal/mol (−17 kJ/mol). This value corresponds to the amount of free energy contributed to the stability of the protein by the salt bridge.
Figure 5. Titration curve between the wild-type (blue) and the mutant (red)

The second method utilizes nuclear magnetic resonance spectroscopy to calculate the free energy of the salt bridge. A titration is performed, while recording the chemical shift corresponding to the protons of the carbon adjacent to the carboxylate or ammonium group. The midpoint of the titration curve corresponds to the pK_a, or the pH where the ratio of protonated:deprotonated molecules is 1:1. Continuing with the T4 lysozyme example, a titration curve is obtained through observation of a shift in the C2 proton of histidine 31 (Figure 5). Figure 5 shows the shift in the titration curve between the wild-type and the mutant in which Asp70 is Asn. The salt bridge formed is between the deprotonated Asp70 and protonated His31. This interaction causes the shift seen in His31’s pK_a. In the unfolded wild-type protein, where the salt bridge is absent, His31 is reported to have a pK_a of 6.8 in H₂0 buffers of moderate ionic strength. Figure 5 shows a pK_a of the wild-type of 9.05. This difference in pK_a is supported by the His31’s interaction with Asp70. To maintain the salt bridge, His31 will attempt to keep its proton as long as possible. When the salt bridge is disrupted, like in the mutant D70N, the pK_a shifts back to a value of 6.9, much closer to that of His31 in the unfolded state.

The difference in pK_a can be quantified to reflect the salt bridge’s contribution to free energy. Using Gibbs free energy: ΔG = −RT ln(K_eq), where R is the universal gas constant, T is the temperature in kelvins, and K_eq is the equilibrium constant of a reaction in equilibrium. The deprotonation of His31 is an acid equilibrium reaction with a special K_eq known as the acid dissociation constant, K_a: His31-H⁺ ⇌ His31 + H⁺. The pK_a is then related to K_a by the following: pK_a = −log(K_a). Calculation of the free energy difference of the mutant and wild-type can now be done using the free energy equation, the definition of pK_a, the observed pK_a values, and the relationship between natural logarithms and logarithms. In the T4 lysozyme example, this approach yielded a calculated contribution of about 3 kcal/mol to the overall free energy.^[4] A similar approach can be taken with the other participant in the salt bridge, such as Asp70 in the T4 lysozyme example, by monitoring its shift in pK_a after mutation of His31.

A word of caution when choosing the appropriate experiment involves the location of the salt bridge within the protein. The environment plays a large role in the interaction.[6] At high ionic strengths, the salt bridge can be completely masked since an electrostatic interaction is involved The His31-Asp70 salt bridge in T4 lysozyme was buried within the protein. Entropy plays a larger role in surface salt bridges where residues that normally have the ability to move are constricted by their electrostatic interaction and hydrogen bonding. This has been shown to decrease entropy enough to nearly erase the contribution of the interaction.[7] Surface salt bridges can be studied similarly to that of buried salt bridges, employing double mutant cycles and NMR titrations.[8] Although cases exist where buried salt bridges contribute to stability, like anything else, exceptions do exist and buried salt bridges can display a destabilizing effect.[3] Also, surface salt bridges, under certain conditions, can display a stabilizing effect.[6][8] The stabilizing or destabilizing effect must be assessed on a case by case basis and few blanket statements are able to be made.

Supramolecular chemistry

Figure 6. The "egg shell" molecular capsule.

Figure 7. Interlacing salt bridges that connect the two halves of the molecular capsule.

Supramolecular chemistry is a field concerned with non-covalent interactions between macromolecules. Salt bridges have been used by chemists within this field in both diverse and creative ways, including the synthesis of molecular capsules and double helical polymers.
Molecular capsules

Molecular capsules are chemical scaffolds designed to capture and hold a guest molecule (see molecular encapsulation). Szumna and coworkers developed a novel molecular capsule with a chiral interior.[9] This capsule is made of two halves, like a plastic easter egg (Figure 6). Salt bridge interactions between the two halves cause them to self-assemble in solution (Figure 7). They are stable even when heated to 60 °C.

Double helical polymers

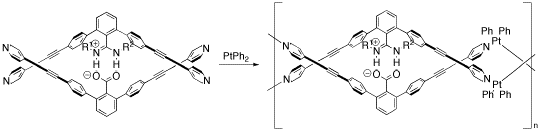
Yashima and coworkers have used salt bridges to construct several polymers that adopt a double helix conformation much like DNA.[10] In one example, they incorporated platinum to create a double helical metallopolymer.[11] Starting from their monomer and platinum(II) biphenyl (Figure 8), their metallopolymer self assembles through a series of ligand exchange reactions. The two halves of the monomer are anchored together through the salt bridge between the deprotonated carboxylate and the protonated nitrogens.

Figure 8. Self-assembly of a double helical metallopolymer.

References

Dougherty, Dennis A. (2006). Modern Physical Organic Chemistry. Sausalito, CA: University Science Books. ISBN 1-891389-31-9.
Al-Haggar M; Madej-Pilarczyk A; Kozlowski L; Bujnicki JM; Yahia S; Abdel-Hadi D; Shams A; Ahmad N; Hamed S; Puzianowska-Kuznicka M (2012). "A novel homozygous p.Arg527Leu LMNA mutation in two unrelated Egyptian families causes overlapping mandibuloacral dysplasia and progeria syndrome.". Eur J Hum Genet. 20 (11): 1134–40. PMC 3476705 Freely accessible. PMID 22549407. doi:10.1038/ejhg.2012.77.
Kumar, S.; Nussinov, R. (2002). "Close-Range Electrostatic Interactions in Proteins". ChemBioChem. 3 (7): 604–617. PMID 12324994. doi:10.1002/1439-7633(20020703)3:7<604::AID-CBIC604>3.0.CO;2-X.
Anderson, D. E.; Becktel, W. J.; Dahlquist, F. W. (1990). "pH-Induced Denaturation of Proteins: A Single Salt Bridge Contributes 3-5 kcal/mol to the Free Energy of Folding of T4 Lysozyme". Biochemistry. 29 (9): 2403–2408. PMID 2337607. doi:10.1021/bi00461a025.
Becktel, W.J.; Schellman, J.A. (1987). "Protein stability curves". Biopolymers. 26 (11): 1859–1877. PMID 3689874. doi:10.1002/bip.360261104.
Horovitz, A.; Serrano, L.; Avron, B.; Bycroft, M.; Fersht, A.R. (1990). "Strength and Co-operativity of Contributions of Surface Salt Bridges to Protein Stability". J. Mol. Biol. 216 (4): 1031–1044. PMID 2266554. doi:10.1016/S0022-2836(99)80018-7.
Dao-pin, S.; Sauer, U.; Nicholson, H.; Mathews, B. W. (1991). "Contributions of Engineered Surface Salt Bridges to the Stability of T4 Lysozyme Determined by Directed Mutagenesis". Biochemistry. 30 (29): 7142–7153. PMID 1854726. doi:10.1021/bi00243a015.
Strop, P.; Mayo, S. L. (2000). "Contribution of Surface Salt Bridges to Protein Stability". Biochemistry. 39 (6): 1251–1255. doi:10.1021/bi992257j.
Kuberski, B.; Szumna, A. (2009). "A Self-Assembled Chiral Capsule with Polar Interior". Chem. Commun. 15 (15): 1959–1961. doi:10.1039/b820990a.
Liu, J.; Lam, J. W. Y.; Tang, B. Z. (2009). "Acetylenic Polymers: Syntheses, Structures, and Functions". Chem. Rev. 109 (11): 5799–5867. PMID 19678641. doi:10.1021/cr900149d.
Ikeda, M.; Tanaka, Y.; Hasegawa, T.; Yashima, E. J.; Yashima, Eiji (2006). "Construction of Double-Stranded Metallosupramolecular Polymers with a Controlled Helicity by Combination of Salt Bridges and Metal Coordination". J. Am. Chem. Soc. 128 (21): 6806–6807. PMID 16719458. doi:10.1021/ja0619096.