.
A Study of Splashes, by Arthur Mason Worthington

A STUDY OF SPLASHES
BY THE SAME AUTHOR.
A FIRST COURSE OF PHYSICAL LABORATORY PRACTICE.
Containing 264 Experiments.
With Illustrations. Crown 8vo, 4s. 6d.
DYNAMICS OF ROTATION.
An Elementary Introduction to Rigid Dynamics.
Crown 8vo, 4s. 6d.
LONGMANS, GREEN, AND CO.
LONDON, NEW YORK, BOMBAY, AND CALCUTTA.
A STUDY OF SPLASHES
BY
A. M. WORTHINGTON
C.B., M.A., F.R.S.
HEADMASTER AND PROFESSOR OF PHYSICS
AT
THE ROYAL NAVAL ENGINEERING COLLEGE, DEVONPORT
WITH 197 ILLUSTRATIONS FROM INSTANTANEOUS PHOTOGRAPHS
LONGMANS, GREEN, AND CO.
39 PATERNOSTER ROW, LONDON
NEW YORK, BOMBAY, AND CALCUTTA
1908
All rights reserved
DEDICATED
TO
THE NATURAL HISTORY SOCIETY OF RUGBY SCHOOL
AND ITS FORMER PRESIDENT
ARTHUR SIDGWICK
IN REMEMBRANCE OF THE ENCOURAGEMENT
GIVEN TO THE EARLY OBSERVATIONS MADE IN BOYHOOD
BY MY OLD SCHOOL-FRIEND
H. F. NEWALL
FROM WHICH THIS STUDY SPRANG.
PREFACE
This publication is an attempt to present in a form acceptable to the general reader the outcome of an inquiry conducted by the aid of instantaneous photography, which was begun about fourteen years ago. The author, in 1894, had occasion to lecture at the Royal Institution on the "Splash of a Drop," of which he had already made a somewhat prolonged study. That lecture, which was subsequently reprinted in the "Romance of Science" series by the Society for Promoting Christian Knowledge, dealt largely with the splash of a drop falling on a solid plate, with which the present volume is not concerned. At the close of the lecture were exhibited for the first time a few photographs of some of the phenomena now dealt with, which the author had just succeeded in taking with the help of his friend Mr. R. S. Cole. The success of the photographs and the additional information they afforded led to a long photographic investigation, which formed the subject of two papers[A] in the Transactions of the Royal Society. Except for two magazine articles,[B] the results of this work have not been presented to the general public. Moreover, in the illustrations printed by the [pg x] Royal Society much of the beauty of the original photographs was lost in the reproduction, or was sacrificed in a selection of which the only object was the elucidation of points of technical scientific interest.
If the present volume is so fortunate as to find many readers among the general public, as the author hopes it may, especially among the young whose eyes are still quick to observe, and whose minds are eager, it will be on account of admiration for the exquisite beauty of some of the forms assumed, of surprise at the revelation of so much where so little was expected, and because of the peculiar fascination that is always felt in following any gradually changing natural phenomenon, in which the sequence of events can, partly at any rate, be anticipated and understood.
For the sake of serious students of Physics who may be interested in unexpected phenomena of fluid motion, all references that seem necessary have been given in footnotes, and it may be mentioned that the later photographs of Series I and those of Series Ia and III, have not been previously published, and afford new information on certain points.
In taking these photographs the author has been much helped by his friends Dr. G. B. Bryan and Mr. G. F. Page.
A. M. W.
Tavistock, Sept. 18, 1907.
[Added March 1, 1908.] A slight delay in the publication of this book has afforded the opportunity of obtaining the new and quite unexpected information given in the supplementary chapter.
FOOTNOTES:
[A] "Impact with a Liquid Surface," by Worthington and Cole. Phil. Trans. Roy. Soc., A 193, 1897, and A 255, 1900.
[B] Pearson's Magazine, July and August, 1898.
CONTENTS
- PAGE
- CHAPTER I
- Preliminary—Methods of Observation and Apparatus 1
- CHAPTER II
- The Splash of a Drop—Low Fall 15
- CHAPTER III
- Principles Involved 32
- CHAPTER IV
- The Splash Continued 41
- CHAPTER V
- Higher Falls—Bubble-Building 53
- CHAPTER VI
- Below the Surface 69
- CHAPTER VII
- The two kinds of Splashes of Solid Spheres 73
- CHAPTER VIII
- The Transition from the Smooth or "Sheath" Splash to the Rough or "Basket" Splash 95
- CHAPTER IX
- The Explanation of the Cause of Difference between the two Splashes 108
- CHAPTER X
- Conclusion 118
- CHAPTER XI
(SUPPLEMENTARY) - A New Phenomenon that appears with an increase in the Velocity of entry of a Rough Sphere 121
A STUDY OF SPLASHES
CHAPTER I
PRELIMINARY—METHODS OF OBSERVATION AND APPARATUS
There will be but few of my readers who have not, in some heavy shower of rain, beguiled the tedium of enforced waiting by watching, perhaps half-unconsciously, the thousand little crystal fountains that start up from the surface of pool or river; noting now and then a surrounding coronet of lesser jets, or here and there a bubble that floats for a moment and then vanishes.
It is to this apparently insignificant transaction, which always has been and always will be so familiar, and to others of a like nature, that I desire to call the attention of those who are interested in natural phenomena; hoping to share with them some of the delight that I have myself felt, in contemplating the exquisite forms that the camera has revealed, and in watching the progress of a multitude of events, compressed indeed within the limits of a few hundredths of a second, but none the less orderly and inevitable, and of which the sequence is in part easy to anticipate [pg 2] and understand, while in part it taxes the highest mathematical powers to elucidate.
In these modern days of kinematographs and snapshot cameras it might seem an easy matter to follow, by the aid of photography, even a splashing drop. But in reality the task is not so simple, for the changes of form that take place in a splash are far too rapid to come within reach of any ordinary kinematograph, and even the quickest photographic shutter is also much too slow, so that it is necessary to have recourse to the far shorter exposure of a suitable electric spark. The originals of the photographs which illustrate this book were taken by means of a spark, whose duration was certainly less than three-millionths of a second, an interval of time which bears to a whole second about the same proportion as a day to a thousand years.
In order to obtain the photographs, advantage was taken of the fact that whatever be the sequence of events in any particular splash, this sequence will be exactly repeated every time that a falling drop strikes the surface under exactly the same conditions, and the problem to be solved was, therefore, as follows:—To cause a drop of definite size to fall from a definite height in absolute darkness so as to strike the surface of the liquid into which it falls at a spot towards which is directed a photographic camera with uncovered lens, and armed with an exceptionally sensitive plate, and to illuminate the drop at the instant that it just touches the surface by a flash of such excessively short duration that no [pg 3] appreciable change of form can take place while the drop is illuminated.
This gives us a photograph of the earliest stage. The plate must then be removed and a fresh one substituted; a second drop, of exactly the same size, must be let fall from exactly the same place, and photographed in just the same way, but the flash must now be so timed as to take place at a slightly later stage of the splash, say, one-thousandth of a second later. The photographic plate must be then again removed and a third substituted, on which a still later stage is to be depicted, and in this way the phenomenon can be followed step by step.
By adopting this process, and not attempting to follow the same individual splash throughout, we avoid two great difficulties: (1) the necessity of shifting our photographic plate or film through a distance equal to the breadth of the whole picture every five hundredth or thousandth of a second (if we wish to obtain pictures of stages so near together as this); and (2) the difficulty of obtaining brilliant flashes of light of sufficiently short duration at these very short intervals.
For these we substitute two other difficulties: (1) that of delivering the drops exactly as required; and (2) that of timing the flash on each occasion within one or two thousandths of a second, so as to pick out the exact stage we wish to photograph.
I will now describe how these two problems have been solved.
It is easy enough to arrange for the production of small drops of almost exactly equal size. They may [pg 4] be allowed to fall one by one at a steady rate from the end of a fine glass tube connected to a vessel in which the liquid is maintained at a constant level, as in Fig. 1, or they may be squeezed out slowly as required by means of a syringe held in a clip as in Fig. 2. Any required number of these small drops can be caught, and allowed to run together if a larger drop is to be experimented with.
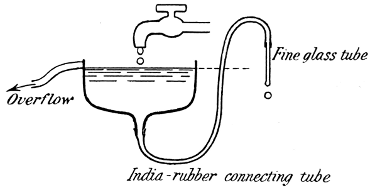
Fig. 1 |
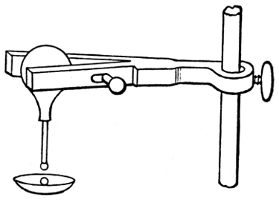
Fig. 2 |
If the liquid used is mercury, the drops may be caught in any little glass cup such as a deeply concave watch-glass; but other liquids, such as water or milk, would wet the glass and stick to it.
If, however, the inside surface of the watch-glass be first carefully smoked in the flame of a candle, then even water or milk will roll over it without sticking, and the drop thus made up will retain a spheroidal form, and can be conveyed to the place of observation in the dark room, where it is transferred to the "dropping cup."
This consists of a similar, deep, smoked watch-glass (W)—see Plate I—supported on the end of a small horizontal lever, a light cylindrical rod of about the dimensions of an ordinary uncut lead [pg 5] pencil, pivoted about a horizontal axle near the end to which the watch-glass is attached. The other end is armed with a small light piece of iron (I) and is held in position by means of an electro-magnet (M), against the action of a spring. On cutting off the current from the electro-magnet the spring, acting as a catapult, tosses up the longer arm of the lever and thus removes the watch-glass from below the drop (D), which is left unsupported in mid-air, so that it falls from a definite fixed distance into a bowl of water placed below it, towards the surface of which the camera (C) is directed. This solves problem number one. Of course, if we wish to observe the splash of a solid sphere, there is no need to smoke the surface of the watch-glass. Indeed, the sphere may be more conveniently supported on a small ring.
Now for the production and timing of the flash. Two large Leyden jars (JJ) are provided, and charged by an electrical machine on their inner coats, one positively and one negatively. Stout wires lead from the outer coats to the dark room, and terminate in a spark-gap (S) between magnesium terminals close over the surface of the water in the bowl just mentioned. If the inner coats are now connected together, the positive and negative charges unite with a dazzling flash and a simultaneous discharge and flash takes place between the two outer coats across the spark-gap in the dark room.
This latter is the illuminating spark; we have now to time it correctly.
For this purpose it is arranged that the discharge [pg 6] shall be effected by means of a falling metal sphere (T) which I shall call the timing sphere, which passes between two terminals S and S connected one to the inside of one jar and one to the inside of the other. These terminals are just too far apart for a spark to leap across, till the timing sphere passes between them and thus shortens the gap; then the discharge takes place, with its accompanying flash in the dark room.
The release of the timing sphere is effected by an arrangement of lever and spring controlled by an electro-magnet exactly similar to that which releases the drop in the dark room, and the two electro-magnets are on the same electric circuit, so that the drop and timing sphere are released simultaneously. But while the drop always falls the same distance, the height through which the timing sphere has to fall before producing discharge can be adjusted at will, and to great nicety, by moving its releasing-lever up or down a vertical support with a scale attached.
If, for example, a particular stage of the splash is photographed when the timing sphere falls just four feet to the gap, then by raising its releasing-lever about two-fifths of an inch, the laws of falling bodies tell us that we shall postpone the flash by just one-thousandth of a second, and the next photograph will accordingly reveal a stage just so much later.
|
PLATE I Arrangement of apparatus for photographing splashes. 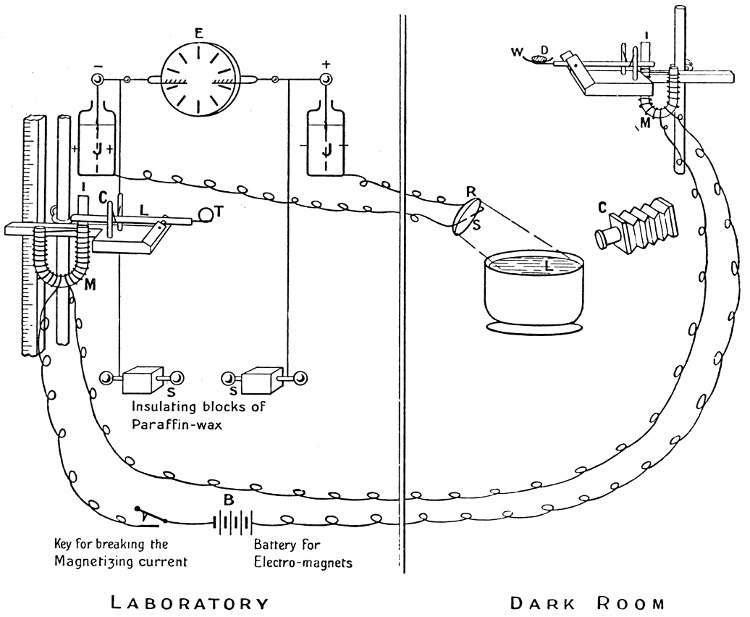 |
|
|
E is the electrical machine. J J are the Leyden jars whose inner coats are connected to the sparking knobs S S. L is the lever for releasing the timing sphere T. C is the catapult. I is the light strip of iron held down by the electro-magnet M. |
D is the drop resting on the smoked watch-glass W. M is the electro-magnet holding down the lever against the action of the catapult, by means of the thin strip of iron I. C is the camera directed towards the liquid L into which the drop will fall. S is the spark-gap between magnesium terminals connected to the outer coats of the Leyden jars. R is the concave mirror. |
It ought still to be mentioned that to make the utmost use of the illuminating power of the spark, it is necessary to place close behind it a little concave mirror (R), by means of which a compact beam of rays, which would otherwise have been wasted, is directed [pg 9] to the required spot. By this addition we imitate, in miniature, the search-light of a man-of-war.
As with all experimental devices, the precision attainable with this arrangement is limited by several circumstances. In the first place, the demagnetization of the iron cores of the electro-magnets, when the current is cut off, is not truly instantaneous, and the time required depends on the strength of the magnetizing current and on the temperature of the iron, which in turn will depend on the length of time for which the current has been running. This variation would be of no importance if the two magnets were exactly alike and the springs of exactly equal strength, conditions which can be nearly but not perfectly fulfilled.
|
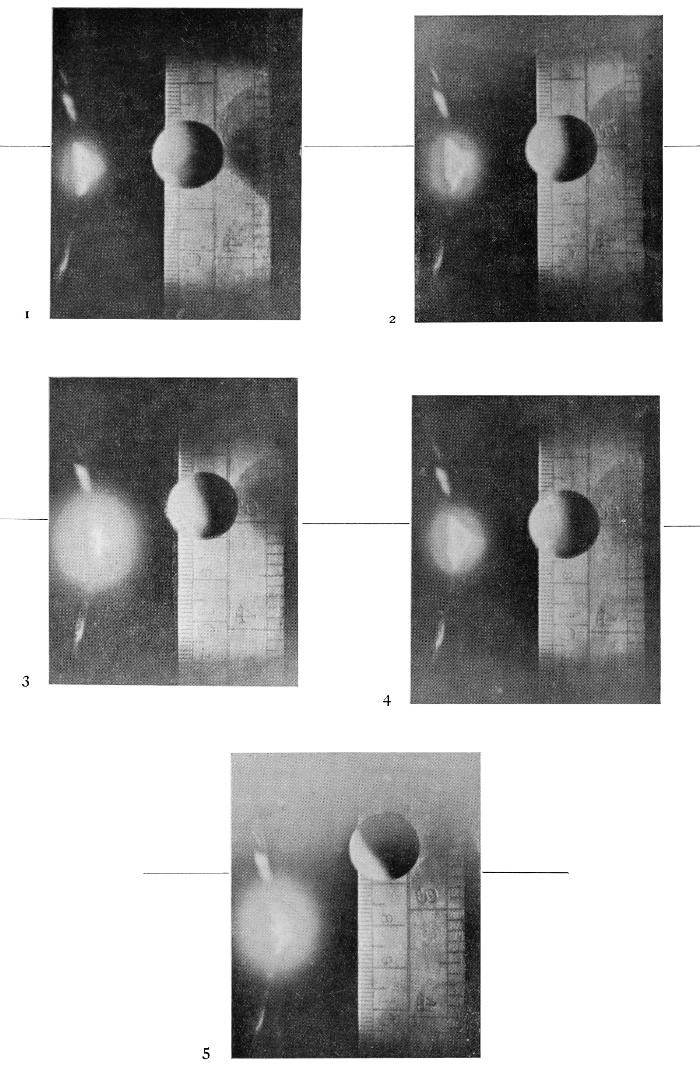
PLATE II Photographs taken to test the accuracy of the "timing." |
||||
 |
||||
A more important source of uncertainty arises from the fact that the time at which the spark takes place depends partly on the magnitude of the + and - charges which have been allowed to accumulate on the discharging knobs connected to the two Leyden jars, for when these charges are larger, then the spark will be longer and will take place earlier and before the timing sphere has reached the mid-position. The charging has therefore to be carefully watched by means of the indications of a suitable electrometer, and the timing sphere must on each occasion be released when the charges have just reached the right value. But even this does not entirely suffice, for the passage of the spark depends also partly on the state of the surface of the knobs, which cannot be kept at any high degree of polish.
[pg 10] Still, when care is taken to keep the conditions as nearly as possible constant, neither of these sources of error is serious, and the reader can judge for himself of the accuracy of the timing from the photographs given on Plate II, in which a solid sphere was let fall in the dark room past a metre scale. The timing sphere was arranged, in the first four photographs, to illuminate it at the same stage in its fall, after a descent of thirty centimetres; if the timing had been perfect the sphere would appear on each occasion at the same mark on the scale.
It will be observed that in the first, second, and fourth photographs the falling sphere is almost accurately bisected by the long line of the three-inch mark on the right-hand edge of the scale. The greatest difference of position being just about one millimetre (as read off the left-hand scale), which would correspond to an error of about 1/2700 of a second. But the third photograph is earlier, showing the sphere 4·5 millimetres higher up, a distance which implies an error of just 1/600 of a second.
A fifth photograph was then taken, with the timing arranged so as to illuminate the sphere one centimetre higher up, and it will be seen that if we compare this with No. 3, the error is again only one millimetre. Thus Nos. 3 and 5 agree very closely, but disagree with Nos. 1, 2, and 4 by about 1/600 of a second.
The photographs themselves supply the reason. For there happens to be visible on each an (out-of-focus) image of the spark, and this image is very much the same in 1, 2 and 4, but much larger and brighter [pg 11] in 3 and 5, showing that the knobs were then more highly charged, which would account for the spark occurring a little too early.
But when we are watching the splash made by the fall of a liquid drop, instead of a solid sphere, there is a new and more serious source of difficulty. For the drop as it lies on the smoked glass cup is not perfectly spherical, but is flattened by its own weight, as shown in Fig. 3, and on the sudden removal of the supporting cup it oscillates between an oval form, elongated vertically, and a flattened form (see Fig. 4). These oscillations are unavoidable, and their extent will depend partly on the amount of adhesion between the smoked surface and the drop, and as this adhesion is never entirely absent and is variable, depending partly on the length of time that the drop has been lying in the cup, it follows that the drop will always receive a slight tug downwards at starting, which will be greater on some occasions than on others. On this account not only will the time taken to reach the water vary slightly, but the drop will strike it sometimes when elongated and sometimes when flattened, and the resulting splash will be affected by this circumstance.
Fig. 3 |

Fig. 4 |
The four photographs on the next page were taken in succession in order to afford the reader an op[pg 12]portunity of judging for himself the sort of accuracy attainable when a liquid drop was concerned.
The fall was 30 centim., and the greatest discrepancy is 4·8 millimetres, corresponding to 1/560 of a second. Thus even here the error does not amount to two-thousandths of a second.
 |
 |
 |
 |
| 1 | 2 | 3 | 4 |
Photographs taken to test the timing of a falling drop.
With higher falls the timing sphere is moving more quickly past the discharging knobs, and the error due to a longer or shorter spark is correspondingly less, so that it appears safe to say that the accuracy of the timing was such that, when all precautions were taken, any desired stage could be picked out within two-thousandths of a second.
It is not however pretended that the precautions necessary for the most accurate timing were always taken, especially in the earlier Series of Photographs, for the main object of the experiments was to find out [pg 13] what happened, and only incidentally to ascertain exactly how long it took to happen, and there is no doubt that on some occasions, through the smoke-film being allowed to wear away, adhesions to the dropping cup occurred, with a corresponding disturbance of the timing, before the defect was noticed and remedied.
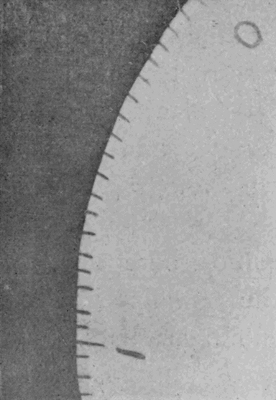
Fig. 5
Photograph of the edge of a rapidly whirling disc.
It remains to mention, for the sake of those interested in photography, that notwithstanding the sensitiveness of the plates and the brilliance of the illuminating spark, its duration was so short that the negatives were always "under-exposed." [C] I have mentioned that the effective duration of the spark was less than three-millionths of a second. The evidence for this is the accompanying photograph (Fig. 5), taken of a cardboard disc when rotating at a rate of fifty-three turns per second; the disc was 22 cm. in diameter, and had been roughly graduated round the edge with pen and ink. The photograph of the part that was in focus shows no perceptible blurring of the edge of the marks, and with a lens, a blurring of one-tenth of a millimetre would be easily detectable. Since the edge was moving at a rate of 36·5 metres per second (about 78 miles per hour), the [pg 14] time taken to traverse one-tenth of a millimetre would be rather less than three-millionths of a second. Hence we may conclude that the illumination did not last so long as this.
The weakness of the negatives was met by a prolonged development of about forty minutes in a saturated solution of eikonogen. This forbade the use of any artificial light, and all the photographic processes had to be conducted in absolute darkness. To avoid the tedium of long waiting in the dark room, a light-tight tray was constructed, in which several developing dishes could be placed, and the whole brought out into the daylight and suitably rocked. In this way ten or twelve photographs could be developed simultaneously.
It may be worth while to mention here that the bright spark given by breaking the primary circuit of an induction coil at the surface of mercury was found to be of much too long duration to be useful for the purposes of splash-photography.
FOOTNOTES:
[C] The plates which I have mostly used have been Thomas's A 1 ordinary.
CHAPTER II
THE SPLASH OF A DROP—LOW FALL
We will now turn to the photographic record itself. The first series shows the splash of a drop of water weighing ·2 of a gram, and therefore 7·36 millimetres (or rather less than one-third of an inch) in diameter, falling 40 cm. (about 16 inches) into milk mixed with water. The object of adding milk to the water was to make it more visible. The addition of milk makes, as we shall see, a little but not much difference in the general character of the splash. The scale of the figures is three-quarters of the actual size.
The number written against any figure gives, on the assumption that no unobserved error has crept in, the time in decimal parts of a second that has elapsed since the stage marked "T = 0," which is nearest to the first instant of contact. The reader will understand from what has been said that the error in any of these times may be as much as two-thousandths of a second, but is not likely to be more than that, when all precautions were taken.
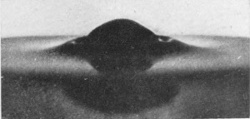
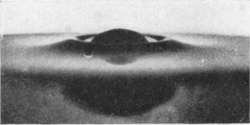
[pg 16] It will be observed that as the drop descends into the liquid the upper portion is at first not appreciably distorted, but that a little cup or crater of liquid is thrown up round it. As the drop descends further, this crater grows wider and higher and thicker in the wall, and jets are shot out from its edge or rim. These jets are visible even in the second figure. The black marks on the inside wall of the crater are due to the lamp-black carried down with the drop from the smoked surface of the supporting cup: though in one sense a disfigurement, they serve to show by their presence that the interior of the crater is lined by the original liquid which formed the drop, and thus afford useful information as to the nature of the flow.
The crater rises with great rapidity up to Fig. 4. In Fig. 5 the walls are beginning to grow thicker, while the next three figures show the crater subsiding and widening, till in Fig. 9 it lies as a mere ring of lobes on the surface, surrounding a central hollow.
SERIES I
Milk into water (40 cm.). Scale 3/4.
|
|
[pg 18] Fig. 10 shows the beginning of the rebound, in the rising of a central column. It will be seen that the lamp-black is now all swept to the middle, indicating that the liquid of the original drop emerges at the head of the central column. Full confirmation of this is obtained from Fig. 12, which represents the emergent column obtained when the circumstances are all the same, except that we have a drop of milk falling into water instead of water falling into milk. It will be observed that the upper part only of the column is visible, precisely because it contains nearly all the milk of the drop, while the lower part, consisting chiefly of transparent water, remains invisible.
SERIES I—(continued)
| 10 0·064 sec. |
 |
| 11 0·073 sec. |
 |
12 | 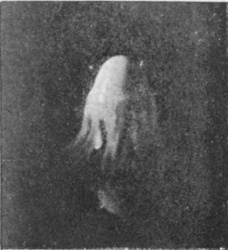 |
| 13 0·093 sec. |
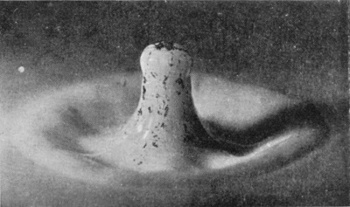 |
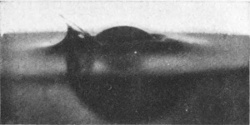
[pg 20] No. 15 shows the column at its greatest height, and it should be noticed that Figs. 16 and 17 show a tendency on the part of the head of this column to split off as a separate drop.
SERIES I—(continued)
| 14 0·103 sec. |
 |
| 15 0·116 sec. |
 |
| 16 0·129 sec. |
 |
[pg 22] The column in subsiding forms a "cake" of liquid round the base. The edge of this circular cake (see Figs. 17, 18, and 19) is the first well-marked ripple spreading outwards in an ever-widening circle.
SERIES I—(continued)
| 17 0·153 sec. |
 |
| 18 0·197 sec. |
 |
| 19 0·217 sec. |
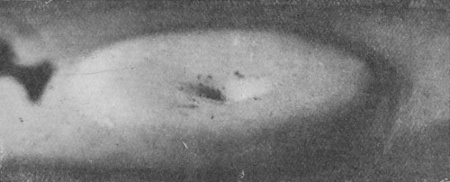 |
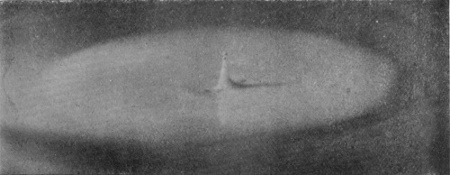
[pg 24] If Fig. 19 is reached without the top of the column having separated, then the splash follows the course shown in Figs. 20a to 23a, in which it will be observed that the disappearance of the first column is very quickly followed by the rise of a secondary column very different in shape, which itself subsides again, but has not yet (in 23a) formed, as it ultimately will, a second "cake" on the top of the first. Thus the second ripple follows late after the first.
SERIES I—(continued)
Alternative (a).
| 20a 0·240 sec. |
 |
| 21a 0·242 sec. |
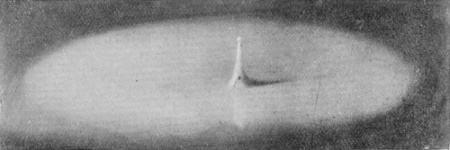 |
| 22a 0·248 sec. |
 |
| 23a 0·253 sec. |
 |
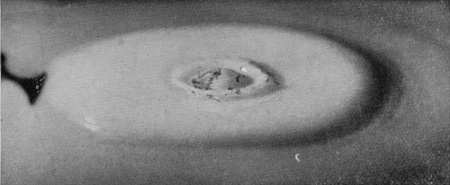
[pg 26] If, however, the summit of the primary column succeeds in breaking off (as in Fig. 18b), or even in very nearly breaking off, then the impact of this newly-formed drop forms a second slight crater on the top of the first cake, and we have the series (18b to 24b), in which it will be observed that the rim of the secondary crater spreads rapidly outwards, so that a second well-marked circular ripple in this case quickly follows the first. The secondary column that is thrown up in Fig. 23b is very like that which emerged at a much earlier stage in the (a) series.
The photographs of this (b) series show very beautifully the manner in which the advancing edge of the ripple degenerates into smaller ripples travelling with greater speed.
SERIES I—(continued)
Alternative (b).
| 18b 0·214 sec. |
 |
| 19b 0·237 sec. |
 |
| 20b 0·242 sec. |
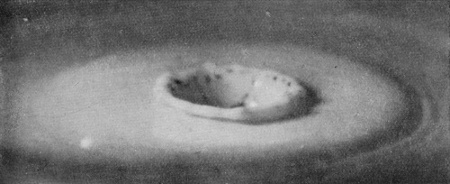 |
| 21b 0·244 sec. |
 |
SERIES I—(continued)
Alternative (b).
| 22b 0·261 sec. |
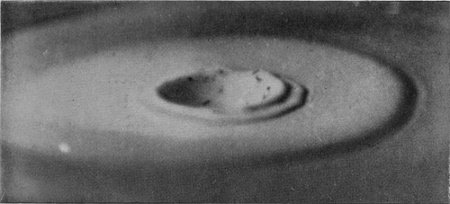 |
| 23b 0·257 sec. |
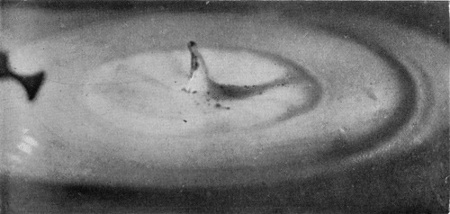
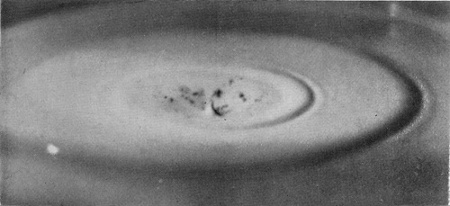 |
| 24b 0·311 sec. |
 |
[pg 30] It will be readily understood that if the splitting off of the head of the primary column happens to take place a little earlier, or on the other hand is nearly, but not quite, complete when it descends below the surface, then subsequent configurations will differ somewhat from either of the sub-series here shown.
Since any figure photographed might belong to either sequence, the disentanglement of the two series required careful consideration and long experimenting.
The reappearance of the original drop at the head of the rebounding column, of which the explanation has been given in this chapter, is easily verified by naked-eye observation.
Let the reader when he next receives a cup of tea or coffee to which no milk has yet been added, make the simple experiment of dropping into it from a spoon, at the height of fifteen or sixteen inches above the surface, a single drop of milk. He will have no difficulty in recognizing that the column which emerges carries the white milk-drop at the top only slightly stained by the liquid into which it has fallen.
In the same way naked-eye observation reveals the crater thrown up by the entry of a big rain-drop into a pool of water. In either case what we are able to glimpse is a "stationary" stage. The rebounding column reaches a maximum height, remains poised for an instant, and then descends. The same is true of the crater. It is the relatively long duration of the moment of poise that produces on the eye a clear impression where all else is blurred by rapid change.
[pg 31] But there is frequently a curious illusion. We often seem to see the crater with the column standing erect in the middle of it. We know now that in reality the crater has vanished before the column appears. But the image of the crater has not time to fade before that of the column is superposed on it.
Those who are accustomed "to believe nothing that they hear and only half of what they see" may be glad to find at least the latter part of their maxim so completely justified.
CHAPTER III
PRINCIPLES INVOLVED
The reader's attention has now been directed to various features which, with certain modifications, will be found in many of the splashes that we shall examine; but so far the language used has been simply descriptive and in no way explanatory. Instead of going on to describe other splashes in the same way, and thus to accumulate a great mass of uncoördinated descriptive detail, it will be better to pause for a moment in order to become acquainted with certain principles connected with the behaviour of liquids, the application of which will go a long way towards explaining what we see going on in any splash.
The first principle to be understood is that the surface layers of any liquid behave like a uniformly stretched skin or membrane, which is always endeavouring to contract and to diminish its area. If the surface is flat, like the surface of still liquid in a bowl, this surface-tension has only the effect of exerting a small inward pull on the walls of the bowl. But if the surface is curved, with a convexity outwards, then the surface layers, on account of their tension, press the interior liquid back, and thus tend to check the growth of any protuberance; while, on the other [pg 33] hand, if the surface is concave outwards, then the surface-tension tends to pull the interior liquid forward, and so to diminish the concavity.
Direct evidence of this surface-tension is easy to cite. We have it in any pendent drop, such as any of those shown in the accompanying figures.
WATER.
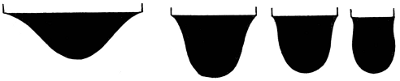
TURPENTINE.

Pendent drops (magnified 2-1/4 times).
If we ask ourselves how it is that the liquid in the interior of one of these drops does not flow out, pressed as it is by the liquid above it, the answer is that everywhere the stretched skin presses it back. A soap-bubble too presses on the air in its interior, both the outside layers and the inside layers of the thin film being curved over the interior space. This is the reason that a soap-bubble blown on the bowl of a pipe will slowly collapse again if we remove the stem of the pipe from our mouth. The bubble drives the interior air back through the pipe. And it is easy to show that if two soap-bubbles be blown on the ends of two tubes which can be connected together by [pg 34] opening a tap between them, then the smaller will collapse and blow out the larger. The reason of this is that in the bubble of smaller radius the surface layers are more sharply curved, and therefore exert a greater pressure on the air within. Thus if a strap be pulled at each end with a total tension T and bent over a solid cylinder of small radius, as in Fig. 6, it is easy to see that the pressure on the surface of the part of the cylinder touched by the strap is less than if the strap be bent over an equal area on a cylinder of larger radius (Fig. 7). The tension of the surface layers of a liquid causes them to act on the liquid within, exactly as does the stretched strap on the solid in these figures. If at any place the liquid presents, as [pg 35] it generally does, not a cylindrical surface, but one with curvature in two directions, then the pressure corresponds to what would be produced by two straps crossing at right angles, laid one over the other, each with the curvature of the surface in its direction (Fig. 8).
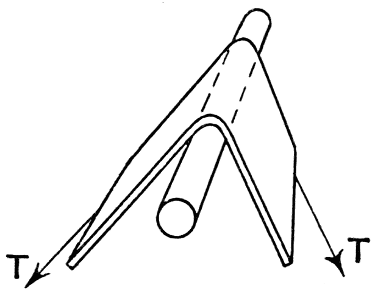
Fig. 6 |
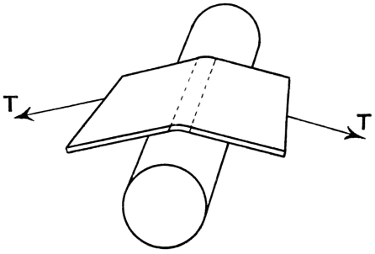
Fig. 7 |
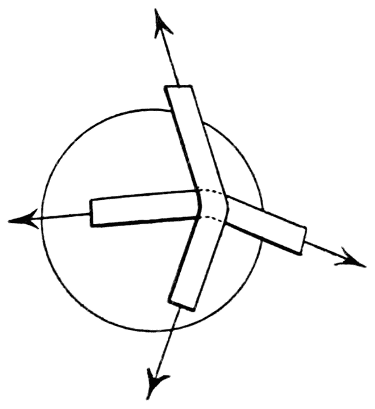
Fig. 8 |

Fig. 9 |
We can now understand why the drop that has been lying on the watch-glass should oscillate in its descent. The sharp curvature of the edge AA of the drop (see Fig. 9) tells us that the liquid there is pushed back by the pressure of the stretched surface layers, and when the supporting glass is removed the sides of the drop move inwards, driving the liquid into the lower part, the tendency being to make the drop spherical, and so to equalize the pressure of the surface at all points. But in the process the liquid overshoots the mark, and the drop becomes elongated vertically and flattened at the sides. This causes the curvature at top and bottom to be sharper than at the sides, and on this account the back-pressure of the ends soon checks the elongation and finally reverses the flow of liquid, and the drop flattens again. As an example of the way in which a concavity of the surface is pulled out by the surface-tension may be cited the dimples made by the weight of an aquatic insect, where its feet rest on the surface without penetrating it.
This same surface-tension checks the rise of the crater, and would cause it to subside again even without the action of gravity. Thus the pressures of the sharply curved crater-edge on the liquid between the [pg 36] crater walls are indicated by the dotted arrows in Fig. 10, and arise from the surface-tension indicated by the full arrows. During the early part of the splash the surface-tension is more important than gravity in checking the rise of the walls. For, as the numbers show, the crater of Series I is already at about its maximum height in No. 4, i.e. about seven-thousandths of a second after first contact. In this time the fall due to gravity would be only about 1/100 of an inch. Thus if gravity had not acted the crater would only have risen about 1/100 of an inch higher. The same reasoning applies to the rise of the central column, but here the curvature at the summit is much less sharp. The numbers show that the column reaches its maximum height in about 5/100 of a second after its start in No. 10, and in this time the fall due to gravity is about half an inch, so that gravity has reduced the height by this amount.
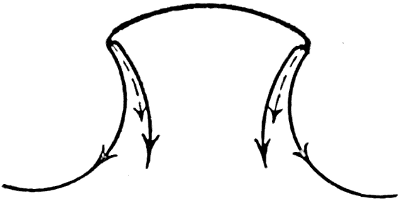
Fig. 10
The second principle which I will now mention enables us to explain the occurrence of the jets and rays at the edge of the crater and their splitting into drops.
It was shown in 1873 by the blind Belgian philosopher, Plateau,[D] that a cylinder of liquid is not a figure of stable equilibrium if its length exceeds about 3-1/7 times its diameter. Thus a long cylindrical [pg 37] rod of liquid, such as Fig. 11, if it could be obtained and left for a moment to itself, would at once topple into a row of sensibly equal, equidistant drops, the number of which is expressed by a very simple law, viz. that for every 3-1/7 times the diameter there is a drop, or that the distance between the centres of the drops is equal to the circumference of the cylinder.

Fig. 11
The cause of this instability is the action of the same skin-tension that we have already spoken of. Calculation shows, and Plateau was able to confirm the calculation by experiment, that if through chance agitations lobes are formed at a nearer distance apart than 3-1/7 times the radius, with hollows between as in the accompanying Fig. 12, then the curvatures will be such as to make the skin-tension push the protuberances back and pull the hollows out. But if the protuberances occur at any greater distances apart than the length of the perimeter, then the sharper curvature of the narrower parts will drive the liquid there into the parts already wider, thus any such an initial accidental inequality of diameter will go on increasing, or the whole will topple into drops.

Fig. 12
[pg 38] At the last moment the drops are joined by narrow necks of liquid (Fig. 13), which themselves split up into secondary droplets (Fig. 14).

Fig. 13
Fig. 14
What we have said of a straight liquid cylinder applies also to an annulus of liquid made by bending such a cylinder into a ring. This also will spontaneously segment or topple into drops according to the same law.[E] Now the edge of the crater is practically such a ring, and it topples into a more or less regular set of protuberances, the liquid being driven from the parts between into the protuberances.
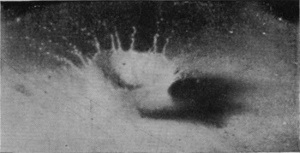
Now while the crater is rising the liquid is flowing up from below towards the rim, and the spontaneous segmentation of the rim means that channels of easier flow are created, whereby the liquid is driven into the protuberances, which thus become a series of jets. These are the jets or arms which we see at the edge of the crater. Examination with a lens of some of the craters will show that the lines of easier flow leading to a jet are often marked by streaks of lamp-[pg 39]black in Series I, or by streaks of milk in Series II. This explanation of the formation of the jets applies also to a similar phenomenon on a much larger scale, with which the reader will be already familiar. If he has ever watched on a still day, on a straight, slightly shelving sandy shore, the waves that have just impetus enough to curl over and break, he will have noticed that up to a certain moment the wave presents a long, smooth, horizontal cylindrical edge (see Fig. 15a) from which, at a given instant, are shot out an immense array of little jets which speedily break into foam, and at the same moment the back of the wave, hitherto smooth, is seen to be furrowed or combed (see Fig. 15b). The jets are due to the segmentation of the cylindrical rim according to Plateau's law, and the ridges between the furrows mark the lines of easier flow determined by the position of the jets.

Fig. 15b |

Fig. 15a |
| Diagrams of a breaking wave. | |
The tendency of the central column of Series I to separate into two parts is only another illustration of the same instability of a liquid cylinder. The column, however, is much thicker than the jets, and its surface is therefore less sharply curved, and consequently the inward pressure of the stretched curved surface is relatively slight and the segmentation proceeds only slowly. Since this segmentation must originate in [pg 40] some accidental tremor, we see how it is that the summit of the column may succeed in separating off on some occasions and not on others. As a matter of fact, the height of fall for this particular splash was purposely selected, so that the column thrown up should just not succeed in dividing in order that the formation of the subsequent ripples might not be disturbed by the falling in of the drops split off. But, as the reader will have perceived, the margin allowed was not quite sufficient.
The two principles that I have now explained, viz. the principle of the skin-tension, and the principle of the instability and spontaneous segmentation of a liquid cylinder, jet, or annulus, will go far to explain much that we shall see in any splash, but it is well that the reader should realize how much has been left unexplained. Why, for example, should the crater rise so suddenly and vertically immediately round the drop as it enters? Why should the drop spread itself out as a lining over the inside of the crater, turning itself inside out, as it were, and making an inverted umbrella of itself? Why when the crater subsides should it flow inwards rather than outwards, so as to throw up such a remarkable central column?
These questions, which demand that we should trace the motion of every particle of the water back to the original impulse given by the impact of the drop, are much more difficult to answer, and can only be satisfactorily dealt with by a complicated mathematical analysis. Something, however, in the way of a general explanation will be given in a later chapter.
FOOTNOTES:
[D] Statique Expérimentale et Théorique des Liquides.
[E] See Worthington on the "Segmentation of a Liquid Annulus," Proc. Roy. Soc., No. 200, 1879.
CHAPTER IV
THE SPLASH CONTINUED
I have stated that the addition of the milk to the water made but little difference in the character of the resulting splash. It does, however, make certain differences in detail, as will be gathered from an examination of the next Series Ia, which shows the effect of letting the water-drop fall from the same height into water instead of into milk. Such a splash is difficult to photograph unless the illumination is from behind. As shown in this way, the early figures of the crater might be unintelligible to the reader had he not already studied the same crater lighted up from the side. Sometimes, though the front of the crater is hardly visible directly, yet every lobe on it can be clearly traced in the inverted image seen by reflection.
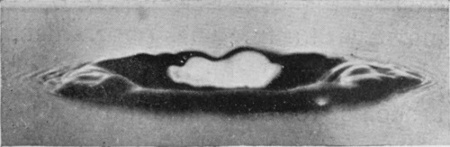
The most noticeable difference between the two splashes is perhaps the very much greater number of ripples seen with the splash in pure water. This is partly because, with the illumination behind, such ripples are more easily visible, but arises chiefly from the fact that ripples are not so readily propagated over the surface of milk on account both of its smaller surface-tension and its greater viscosity. The first appearance of outward-spreading ripples is in No. 6, just round the subsiding crater.
SERIES Ia
Water into water (40 cm. fall). Scale 9/10.
| 1 T = 0 |
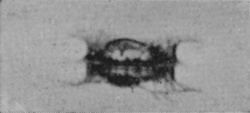 |
| 2 0·004 sec. |
 |
| 3 0·013 sec. |
 |
| 4 0·018 sec. |
 |
SERIES Ia—(continued)
| 5 0·026 sec. |
 |
| 6 0·042 sec. |
 |
| 7 0·058 sec. |
 |
| 8 0·073 sec. |
 |
[pg 44] Since the origination of these ripples is an interesting phenomenon from a physical point of view, as throwing light on the dispersion of waves travelling with different velocities, special precautions were taken to secure the most favourable conditions, and in order to clean the surface after the arrival of each drop, which inevitably brings down a little adherent lamp-black, a continuous slow stream of fresh water was maintained which swept the contaminated surface-liquid away over the edge of the vessel.
The effect of this precaution is seen by a comparison of the photographs No. 11 and No. 11a. In the first the surface was kept quite clean in the way described; in the second it had only been cleaned by skimming it with a fine wire-gauze dish.
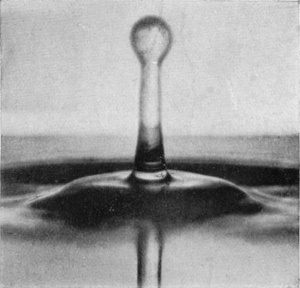
The beginning of the descent of the first central column seems to be marked by the appearance of a slight depression round its base, which has just not begun in No. 11a, and has just begun in No. 11, and goes on increasing in Figs. 12 and 13.
SERIES Ia—(continued)
Running water. Scale reduced to 6/10.
| 9 0·087 sec. |
 |
| 10 0·014 sec. |
 |
| 11 0·139 sec. |
 |
11a 0·139 sec. |
 |
SERIES Ia—(continued)
Running water. Scale 6/10.
| 12 0·163 sec. |
 |
13 0·185 sec. |
 |
| 14 0·207 sec. |
 |
| 15 0·227 sec. |
 |
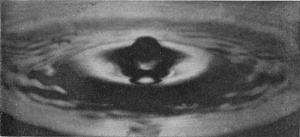
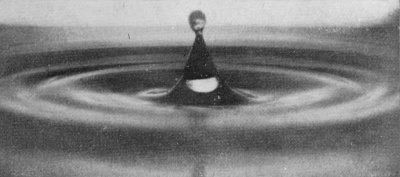
[pg 48] The same feature marks the beginning of the descent of the secondary central column, which is still rising in Fig. 17, is just poised in Fig. 18, and thence onwards shows a gradually increasing central depression. These last four figures carry us to a rather later stage than was reached in Series I.
It should be noticed that in this Series the water-drop used was of smaller diameter than that of Series I, weighing ·13 grams as against ·2 grams. By employing the smaller drop, we diminish irregularities due to oscillations of form set up on release, for the smaller drop is more spherical when lying on the dropping cup than the larger; a few photographs taken for comparison with the full-sized drop showed, however, extremely little difference in the splashes at this height of fall.
SERIES Ia—(continued)
Still water. Scale 9/10.
| 16 0·247 sec. |
 |
| 17 0·266 sec. |
 |
| 18 0·294 sec. |
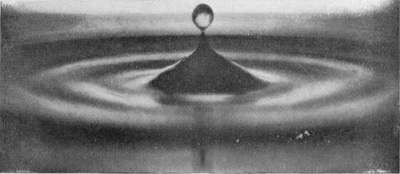 |
SERIES Ia—(continued)
Still water. Scale 9/10.
| 19 0·285 sec. |
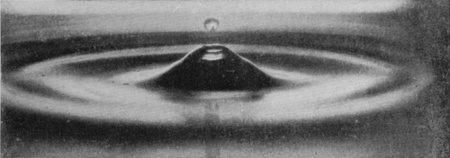 |
| 20 0·311 sec. |
 |
| 21 0·321 sec. |
 |
CHAPTER V
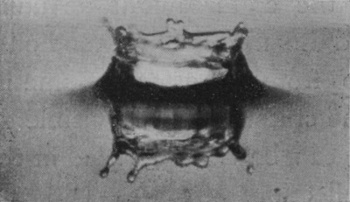
HIGHER FALLS—BUBBLE-BUILDING
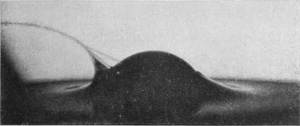
It might well be expected that the effect of increasing the height of fall of our drop to 100 cm. would be simply to emphasize the phenomena already observed, and to obtain a higher crater and a taller rebounding column. Such an expectation would be mistaken. A new phenomenon makes its appearance. The crater does indeed rise to a greater height, but its mouth closes so as to form a bubble on the surface of the liquid. If the height be not too great the closing is either incomplete or at any rate only temporary, and the bubble reopens at the top to make way for the column which rises as before from the base, but is now much thicker and hardly so high as before.
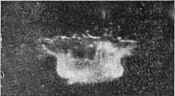
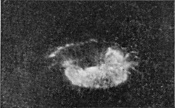
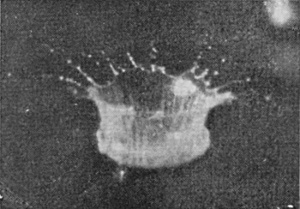
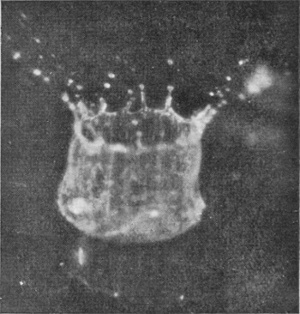
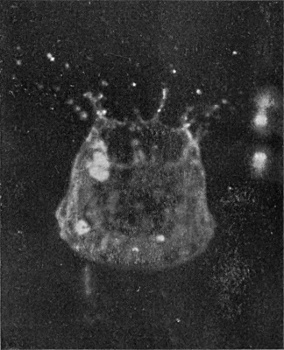
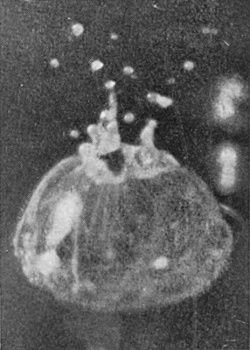
In the Series II, which is now given, the drop was of milk, 7·36 mm. in diameter, and fell 100 cm. into water.
Photographs 1 and 2—to which is added 2a, though taken under slightly different conditions—show that the drop on entering punches a sheer-walled hole, for the fine line of light seen above the level of the top of [pg 54] the drop in Figs. 2 and 2a marks the circular cliff-like edge of the as yet undisturbed liquid. Up the vertical sides of this circular pit the liquid of the drop is streaming. This cliff is highest and perhaps clearest in Fig. 2a.
The closing of the mouth of the crater, which is just beginning in Fig. 5, is to be explained as follows. If the crater were a simple thin-walled cylinder of liquid, it would contract under the influence of the surface-tension just as does a soap-bubble, but not so fast, since the walls have only a horizontal curvature. If the wall is thinner above than below, then the upper part will contract faster than the lower, through there being less liquid to accelerate. Now the supply of liquid is from below, and will thicken the lower part of the walls first, and thus account for the faster closing of the mouth. On the other hand, the uppermost edge of the crater is the place where the checking influence of the surface-tension on the upward flow is first felt, with the result that the edge of the rim is thickened by the influx from below, so that a more or less regular rope-like annulus is formed round the edge. Now calculation shows that such an annulus, so long as its thickness is not more than 1·61 times the thickness of the wall below, will contract quicker than the wall, and this will tend to close the crater, somewhat as a bag would be closed by the contraction of an elastic cord round the mouth. This rope-like thickening of the edge is to be seen in Figs. 5 and 7, and especially in Figs. 3 and 4 of Series III on page 63.
SERIES II
Milk into water (100 cm. fall).
| 1 0·002 sec. |
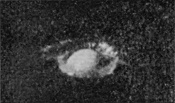 |
2a | 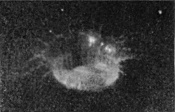 |
3 0·002 sec. |
 |
| 2 0·002 sec. |
 |
| 4 0·009 sec. |
 |
5 0·018 sec. |
 |
| 6 0·018 sec. |
 |
7 0·039 sec. |
 |
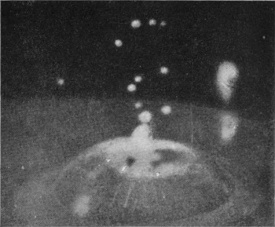
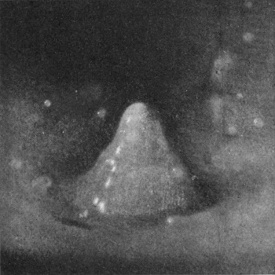
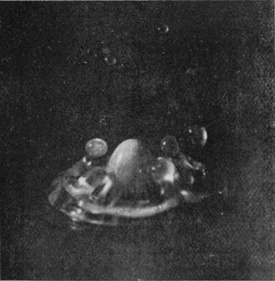
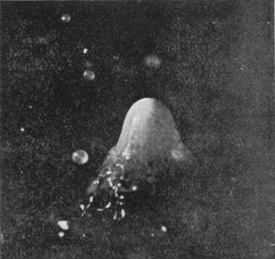
[pg 56] The photographs 9, 10, and 11 (obtained after adding a little milk to the water in order to render it more visible) were at first very puzzling. What happens is that the bubble sometimes reopens very soon (or perhaps does not quite close) as in Fig. 9, and makes way for the column which rises from the base exactly as in the previous series. This column may be dimly seen through the walls of the bubble in Fig. 9, and No. 10 shows the column alone, the bubble having opened early and receded with great velocity, a few drops round the base being all that is left of it. Nos. 10a and 10b illustrate this reopening. In 10a the milk-drop was allowed to fall again into quite pure water, and the photograph shows very beautifully the summit of the column, with the original milk-drop at the top, emerging through the reopening mouth of the bubble; and Fig. 10b shows the same at a very slightly later stage when the bubble has completely retreated.
SERIES II—(continued)
| 8 0·054 sec. |
 |
9 0·085 sec. |
 |
| 10 0·105 sec. |
 |
| 10a 0·103 sec. |
 |
10b 0·111 sec. |
 |
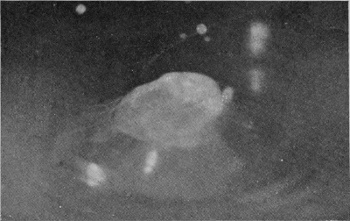
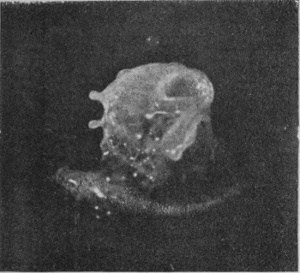
[pg 58] In Fig. 11 the bubble has been too firmly closed to reopen, and the summit has been struck by the column within. The next figure (No. 12) shows how in such a case the emergent column becomes entangled in the liquid of the bubble when it bursts. Under the influence, however, of the surface-tension, which pushes back the protuberances and pulls out the hollows, regularity of form is soon regained. Thus Fig. 13 shows the emergent columns at a later stage after such an encounter, already much more symmetrical; and the subsequent photographs (for which a good deal of milk was added for the sake of greater visibility) show a column of uniformly sedate and respectable rotundity, betraying no traces of any youthful irregularities.
SERIES II—(continued)
| 11 0·105 sec. |
 |
| 12 0·095 sec. |
 |
13 0·113 sec. |
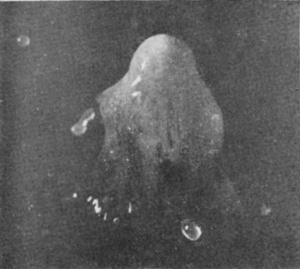 |
| 14 0·132 sec. |
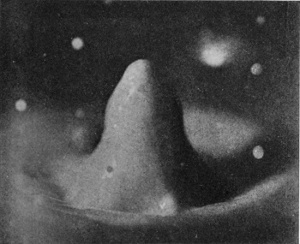 |
15 0·194 sec. |
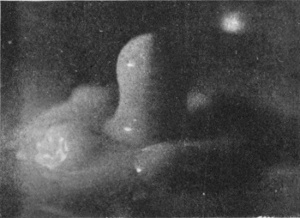 |
SERIES II—(continued)
| 16 0·217 sec. |
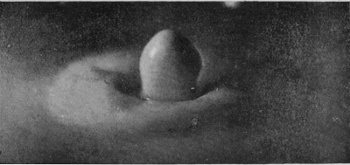 |
| 17 0·240 sec. |
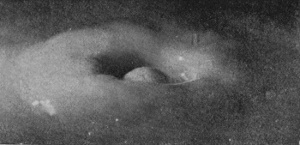 |
| 18 0·272 sec. |
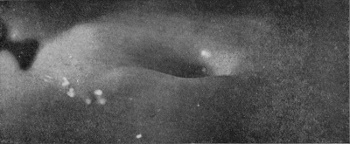 |
| 19 0·311 sec. |
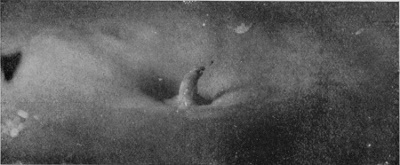 |
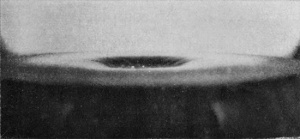
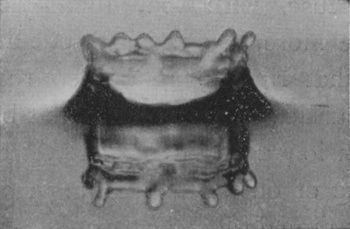
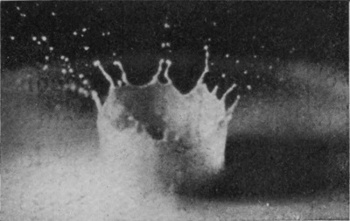
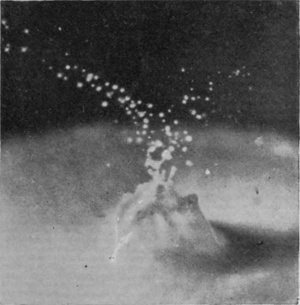
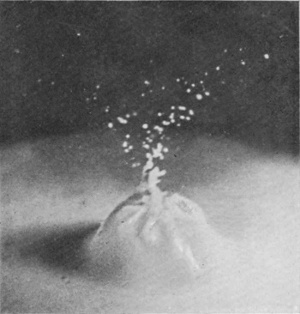
[pg 62] Series III shows the effect of still further increasing the height of fall of the water-drop (to 137 cm., or about 4 ft. 6 in.), and at the same time doubling its volume so that it now weighs ·4 gram. The crater now closes in about 18/1000 of a second, and forms a comparatively permanent bubble. The rope-like thickening of the edge, already alluded to, is well seen in Figs. 3 and 4. In its earlier stages the bubble is thick-walled, rough, and furrowed, but becomes smoother and thinner the longer it lasts, both because the liquid drains down the sides and because it becomes more uniformly distributed under the equalizing influence of the surface-tension.
SERIES III
Water-drop weighing 0·4 grams falling 137 cm. (4-1/2 feet) into milk mixed with water. Scale 1/2.
| 1 T = 0 |
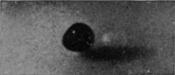 |
2 0·005 sec. |
 |
| 3 0·016 sec. |
 |
| 4 0·019 sec. |
 |
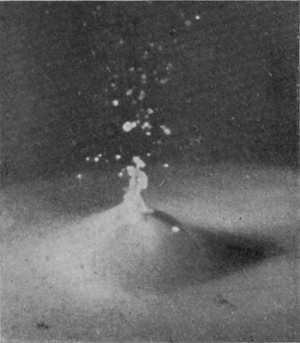
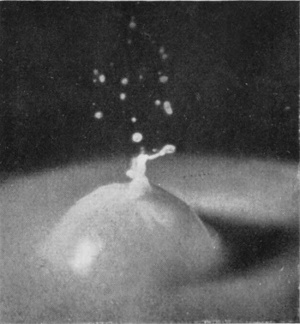
[pg 64] Such a bubble may remain long closed, as in Fig. 8, becoming every moment more delicate and exquisite, or it may open at an even earlier stage, as in Fig. 9.
There is a characteristic difference between the arms of a closing and of an opening bubble. It will be noticed that up to the moment of closing the arms slope outwards. The upper portions have been projected at an earlier stage when the mouth of the crater was wider open and the flow was either actually outwards or more nearly vertical; then as the mouth contracts the arms are left behind in the upper parts.
SERIES III—(continued)
| 5 0·017 sec. |
 |
6 0·020 sec. |
 |
| 7 0·036 sec. |
 |
8 0·053 sec. |
 |
[pg 66] In an opening bubble, on the other hand, the arms are at first vertical, and later have the very characteristic inward slope of the last figure, which is also well seen in Fig. 10a of the last series. Here the edge of the opened bubble retreats outwards and downwards, leaving the arms behind.
Such is the origin of the bubbles raised by the big drops of a thunder shower on the surface of a pool. The building of each fairy dome is accomplished in less than two-hundredths of a second, and before one-tenth of a second has elapsed the whole construction may have vanished. One can almost regret that so beautiful a process should have been so long unwatched.
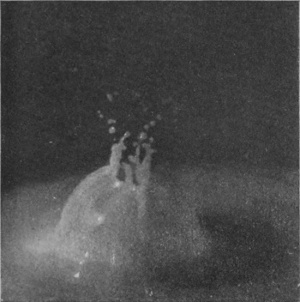
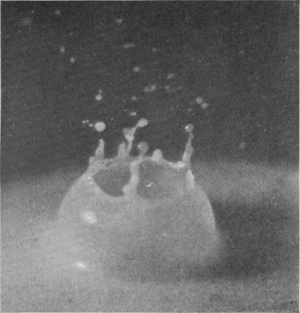
To build these bubbles a large drop is essential. With a drop weighing only 0·4 of a gram, even though it fall from a height of 177 cm., there is no bubble, and the splash is almost exactly that of Series Ia. The exact time required for the closing of the bubble probably depends a good deal on the phase of oscillation of the drop at the moment of entry, and, as already observed, a big drop, which lies very flat in the dropping cup, is set vibrating more strongly on liberation than a small one.
We shall see in Chapter VII that the impact of a rough solid sphere, if falling from a sufficient height, produces a very exquisite bubble; in this case irregularities due to oscillation are absent, and the closing can be timed with greater precision.
SERIES III—(continued)
| 9 0·040 sec. |
 |
10 0·046 sec. |
 |
| 11 0·070 sec. |
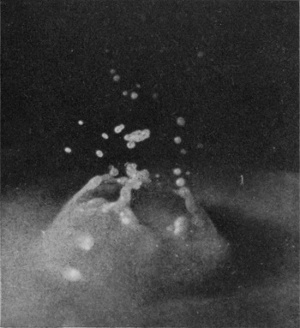 |
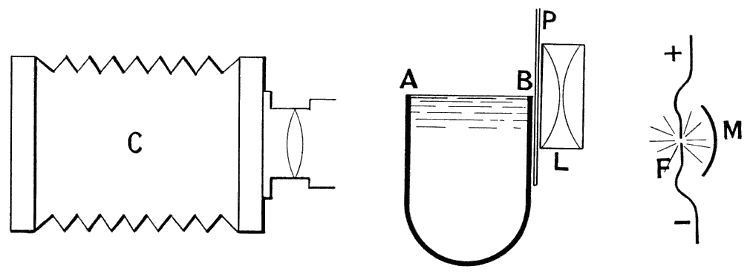
Fig. 16
Arrangement for taking photographs below the surface of the liquid.
CHAPTER VI
BELOW THE SURFACE[F]
Our investigation has so far been limited to what we can see from above the surface of the liquid; nor perhaps would it occur to any one acquainted only with so much as we have yet examined that it might be worth while to look below the general level of the surface. The discovery, however, that when the splash is made by a solid sphere very remarkable phenomena, which will be described in the next chapter, take place below the surface, led at a much later date to a similar examination in the case of a liquid drop.
A suitable arrangement of the apparatus in the dark room is shown in the accompanying diagram (Fig. 16).
The water into which the drop is to fall is placed in a thin glass vessel AB, with parallel sides. (An inverted clock-shade makes a very convenient vessel.) The water fills the vessel to the brim, and is allowed to overflow it in a steady stream, thus presenting a surface which, being perpetually renewed, is maintained perfectly clean. Close behind the vessel is a plate P of finely roughened glass, on which the light from the spark-gap F, in front of its concave [pg 70] reflector M, is thrown by means of the condenser lens L taken from an optical lantern. This provides a very uniformly illuminated background against which the splash is viewed by means of the camera C, whose optic axis is horizontal, either a little below the level of the liquid surface or at that level. By having it just at the level of the surface we secure simultaneous pictures of what is going on both above and below the surface. There is, to be sure, a narrow band or region of confusion stretching across the photographs in which the images obtained by reflection, both external and internal, overlap the direct images, and it should also be mentioned that the two pictures will not be quite in focus together, for the optical effect of the water, through which the part below the surface is viewed, is to bring the image forward.
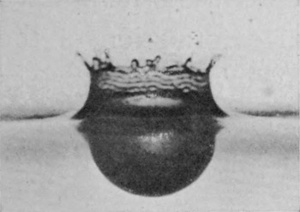
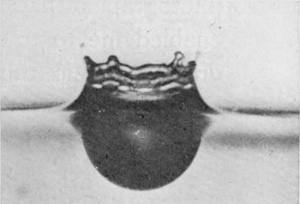
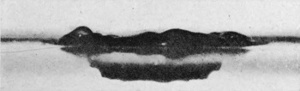
The photographs of Series IV were obtained in this way from the splash of a drop of water weighing 0·176 grams falling 40 cm. into water. (The same splash as that of Series Ia.) The perfectly spherical form presented by the cavity below the surface is very remarkable. In the present case, this spherical cavity when at its deepest, as in Fig. 5, would contain about fifty of the original drops, and in other cases—e.g. with a drop of 1/4 the volume, falling from 177 cm.—the cavity would contain as many as 360 of the original drops.
In Figs. 5, 6, and 7 the depth of the cavity is nearly constant, but the diameter is steadily increasing. The spherical form, however, is still maintained. The last figure shows the central column just beginning to rise.
SERIES IV
The splash of Series Ia viewed below the surface.
| 1 |  |
2 T = 0 |
 |
3 0·009 sec. |
 |
| 4 0·012 sec. |
 |
5 0·016 sec. |
 |
| 6 0·023 sec. |
 |
7 0·039 sec. |
 |
| 8 0·055 sec. |
 |
| 9 0·070 sec. |
 |
[pg 72] There can be no doubt that the liquid of the original drop is spread out in an excessively thin lining over the interior of this sphere. The reader has seen for himself part of the evidence in the streaks of milk that are carried up the inner walls of the crater when a milk-drop falls into water (Series II); in the streaks of lamp-black that are carried there when the drop is of milk, and it may here be mentioned that other photographs that cannot be reproduced here have enabled me to trace the gradual deformation of the drop into this thin layer and show that it passes through configurations like Figs. 17, 18, and 19.
 Fig. 17 |
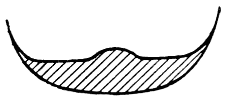 Fig. 18 |
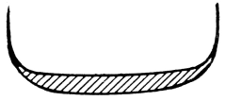 Fig. 19 |
It appears possible that the study of this remarkable spherical excavation may afford a clue that will lead to a solution of the very difficult hydro-dynamical questions involved, and the matter is still being investigated.
FOOTNOTES:
[F] The information conveyed in this chapter was first published in a communication to the Mathematical and Physical Section of the British Association at Leicester in 1907.
CHAPTER VII
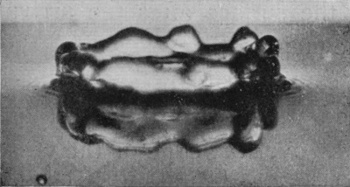
THE TWO KINDS OF SPLASHES OF SOLID SPHERES
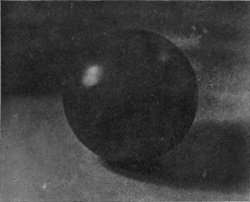
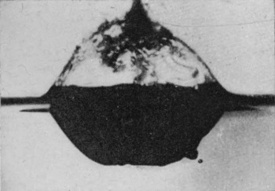
In the present chapter will be described the splash that follows the entry of a solid sphere falling vertically into a liquid from a small height, and I should like to persuade the reader, if possible before he begins to read, or at any rate afterwards, to make a very simple experiment. Let a few child's marbles be taken—not glass "marbles," for these are seldom round enough or smooth enough, but what are sold in the toy-shops as "stone" marbles—and let one of these be well rubbed and polished with a dry handkerchief, and then dropped from a height of about 30 cm., or, say, 1 foot, into a deep bowl or basin of water, the bottom of which may be conveniently protected from breakage by a few folds of fine copper gauze.
If the polishing has been good, and the surface of the sphere has not been dimmed by subsequent handling with hot or greasy fingers, it will be observed that the splash is singularly insignificant, the sphere [pg 74] slipping noiselessly into the liquid with very little disturbance of the surface.
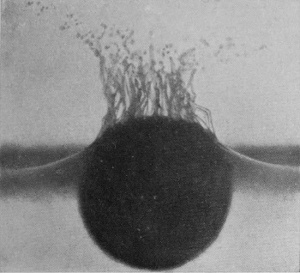
But if the same sphere be fished out of the water, and again let fall from the same height without being first dried, or, better still, if another marble be taken, which has been previously roughened with sand-paper, the resulting splash is totally different. There is now a noise of bubbles, which may be seen rising through the liquid, and a tall jet is seen to be tossed into the air.
(1) THE SPLASH OF A ROUGH SPHERE.
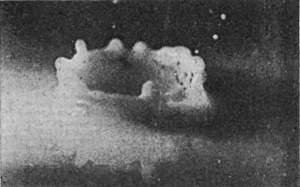
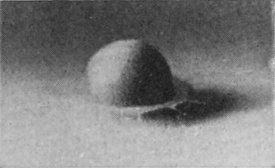
To understand the cause of this really surprising difference we must turn to the photographic record, and we will take first the case of a rough sphere falling into water to which milk has been added for the sake of clearness in the photographs. The diameter of the sphere was 1·5 cm. (or 3/5 inch), and the height of fall 15 cm., or just about 6 inches. The sphere on each occasion was fished out, redried, and re-roughened with sand- or emery-paper. Examination of the first photographs of Series V shows that the liquid, instead of flowing over and wetting the surface of the sphere, is driven violently away, so that as far as can be seen from above the upper portion is, at first at any rate, unwetted by the liquid. The crater that is subsequently formed is very similar to that which was thrown by the liquid drop in Series I, the main difference being that in the present-case the crater is thinner in the wall and more regular. This greater regularity is chiefly to be attributed to the fact that [pg 76] the solid sphere enters the liquid with a true spherical form, and is not distorted by the oscillations and tremors which disturb a falling drop. The gradual thickening of the wall and the corresponding reduction in the number of lobes as the subsidence proceeds is beautifully shown in Figs. 7, 8, 9, and 10, the last-mentioned figure being hardly distinguishable from the corresponding Fig. 9 of Series I, p. 17. This stage is in each case reached in about 58/1000 of a second.
SERIES V
Rough sphere. "Basket splash."
Diameter of sphere, 1·5 centim. Height of fall, 15 centim.
| 1 T = 0 |
 |
| 2 0·003 sec. |
 |
| 3 0·006 sec. |
 |
| 4 | 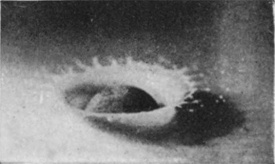 |
| 5 | 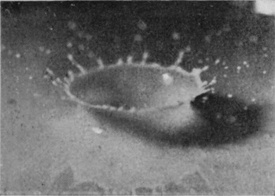 |
6 | 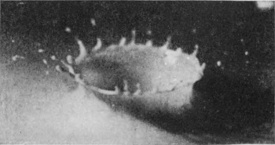 |
SERIES V
Rough sphere—(continued).
| 7 0·024 sec. |
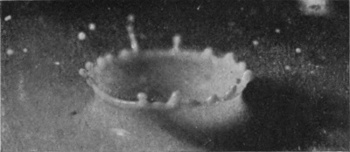 |
| 8 0·032 sec. |
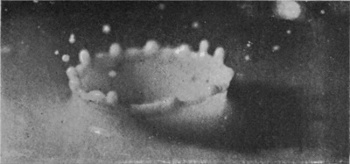 |
| 9 0·042 sec. |
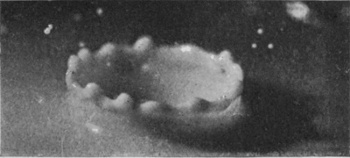 |
| 10 0·060 sec. |
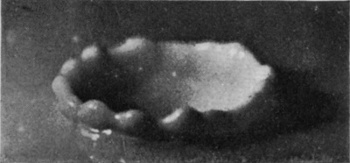 |
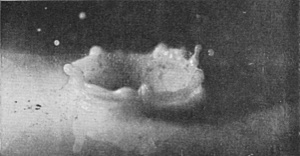
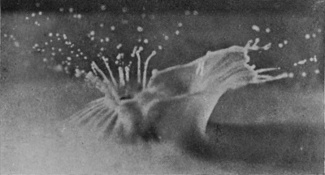
[pg 78] Now from the depths of the crater there rises with surprising velocity the exquisite jet of Fig. 11, which in obedience to the law of segmentation at once splits up in its upper portion into little drops, while at the same time it gathers volume from below, and rises ultimately as a tall, graceful column to a height which may be even greater than that from which the sphere fell. This is the emergent jet which one sees with the naked eye whenever a sufficiently rough sphere is dropped from a small height into water, but if we are to ascertain how this column originates, we must follow the sphere below the surface of the liquid. The arrangement already described on p. 69 enables this to be done. We let the sphere fall into clear water contained in a narrow, flat-sided, inverted clock-shade and illuminate this from behind while the camera stands straight in front.
SERIES V
Rough sphere—(continued).
| 11 0·068 sec. |
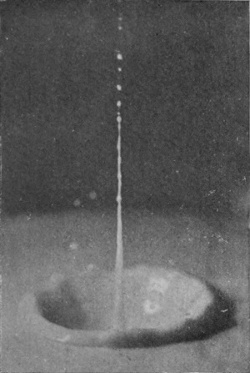 |
12 0·076 sec. |
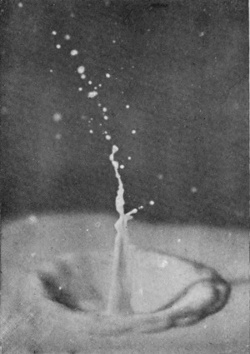 |
| 13 0·088 sec. |
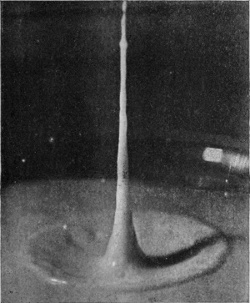 |
14 0·100 sec. |
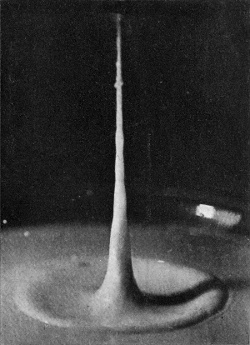 |
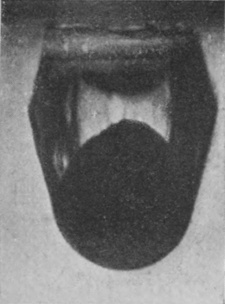
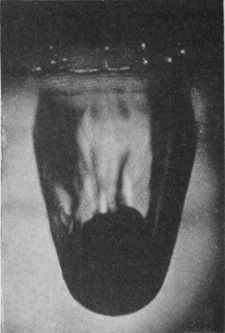
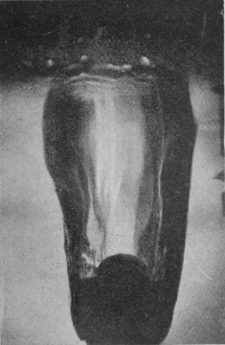
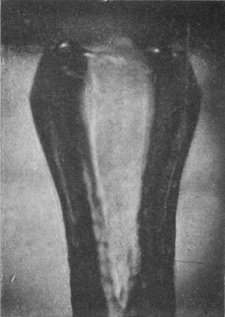
[pg 80] In this manner were obtained the photographs of Series VI, which require a little explanation. In the first figure we see the sphere just entering the liquid. The faint horizontal line shows the level of the surface. Above this line we see the internally reflected image of the part that has already entered, while still higher in the figure may be discerned the summit of the sphere itself. The slight lateral displacement of the part below the surface is due to refraction consequent on the camera having been set with its optic axis not quite perpendicular to the face of the vessel. In the subsequent figures it will be observed that the sphere, as it descends, drags with it the surface of the liquid in the form of a gradually deepening pocket or bag, the upper part of the sphere being for a long time quite unwetted by the liquid.
The sides of this pocket or bag of air not being quite smooth, give a somewhat distorted appearance to the sphere within. Also, since the sides are sloping, their reflected image in the level surface slopes in the opposite direction and produces an angle where the two meet. This angle marks very clearly the level of the surface. Above the surface-line in Figs. 2 to 5 is seen the beaded lip of the crater which we have already viewed from above, but this is somewhat out of focus, for the camera had to be focused on the sphere as seen under water, and the effect of the water is to bring the sphere optically nearer. Hence only the nearer part of the crater, i.e. the middle part of the front edge, is distinctly shown.
SERIES VI
The splash of a rough sphere as seen below the surface.
Diameter, 1·5 centim. Height of fall, 15 centim.
| 1 T = 0 |
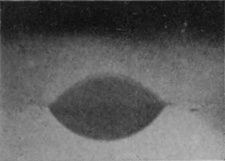 |
2 0·010 sec. |
 |
3 0·018 sec. |
 |
| 4 0·023 sec. |
 |
5 0·032 sec. |
 |
[pg 82] Coming now to Fig. 6, we perceive that the long cylindrical hollow has begun to divide. In this spontaneous division we have another illustration of the law of instability which regulated the sub-division of the jets and columns of earlier series. This law is the same whether the cylinder be of air surrounded by liquid or of liquid surrounded by air. Hitherto we have only seen it operating in jets of liquid in air; now we have a jet of air in a liquid.
The lower part of the long cylinder of air splits off into a bubble just behind the sphere, and follows in its wake to the bottom of the vessel, and is only detached and rises to the surface when the sphere strikes the bottom. Many years ago, through the kindness of the curator of the Brighton Aquarium, I was enabled to watch this bubble of air following in the wake of the sphere to the bottom of the deepest tank.
Figs. 7, 8, and 9 show the two parts gradually separating.
SERIES VI—(continued)
Scale reduced to about 7/10.
| 6 0·045 sec. |
 |
7 | 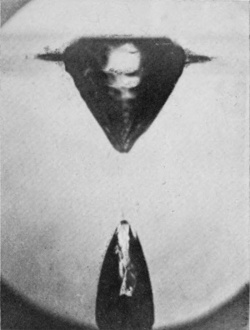 |
| 8 0·050 sec. |
 |
9 0·054 sec. |
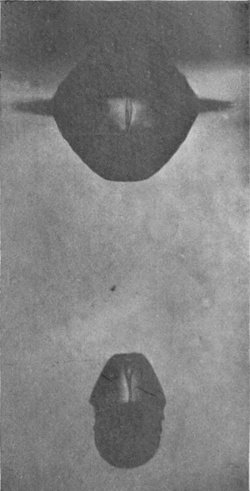 |
[pg 84] Fig. 10 shows specially well the ripples on the surface of the descending bubble. These undulations sometimes become so accentuated that the upper part of this descending bubble is detached, and then the curious phenomenon may be seen of this detached part still following the rest downwards through the liquid with an unsteady, lurching motion.
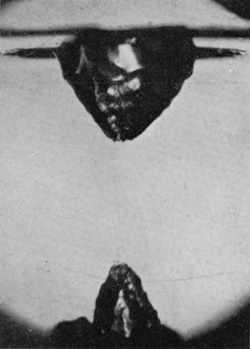
Meanwhile the upper half of the divided air-column is seen in Fig. 9 to resemble a deep basin which now rapidly fills up by the influx of liquid from all sides. It is from the confluence of this inflowing liquid into channels which necessarily narrow as the centre is approached that the great velocity with which the liquid spirts upwards is obtained. In Fig. 11 the jet is just discernible above the surface, and in Fig. 13 it is well-established.
SERIES VI—(continued)
| 10 0·062 sec. |
 |
| 11 | 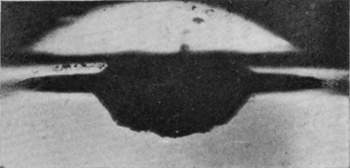 |
| 12 0·062 sec. |
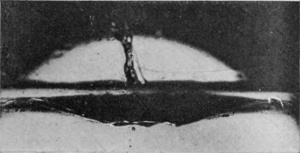 |
13 0·070 sec. |
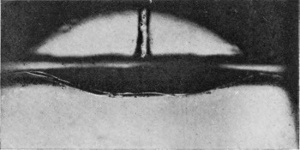 |
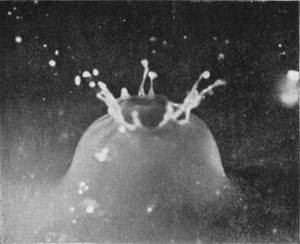
[pg 86] On increasing the height of fall of a rough sphere to 60 cm., we obtain a higher crater which closes and forms a bubble, exactly as when we increased the height of fall of a liquid drop. The process as viewed from above the surface is shown in Series VII. The first figure of this series shows very well how completely the liquid is driven away from the surface of the sphere the first moment of contact. The subsequent crater and bubble are of exquisite delicacy. This bubble, though it closes completely as in the last figure, is doomed to almost immediate destruction. For we see, on looking below the surface, that the proceedings there are of the same kind as in the case of the lower fall already described, and result in the formation of an upward-directed jet.
SERIES VII
Rough sphere falling 60 cm. Scale 3/4.
| 1 T = 0 |
 |
| 2 0·003 sec. |
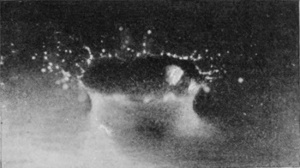 |
| 3 0·017 sec. |
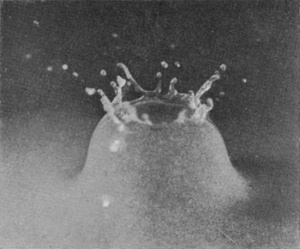 |
4 0·017 sec. |
 |
| 5 0·033 sec. |
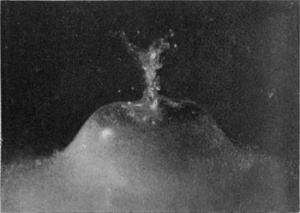 |
[pg 88] Thus the first three figures of Series VIII show the last moments of a bubble which has burst, spontaneously, and so has made way for the jet of Fig. 3. (These are taken from a splash into petroleum with 24·5 cm. fall.) But the last two figures, 4 and 5 (taken with a 32 cm. fall), show how a bubble which might otherwise have been permanent, is stabbed by the rising jet and destroyed. With water and 60 cm. fall the jet appears sometimes to rise quite unimpeded, and sometimes to be checked by the still closed bubble.
Before leaving the splash of a rough sphere, I desire to call the reader's attention to another point.
Such figures as 7, 9, and 10 of Series V, p. 77, show that the surface of the liquid beyond the walls of the crater is still flat and undisturbed; yet we now know from the corresponding Figs. 5, 6, and 7 of Series VI, p. 83, that a large volume of liquid has been displaced, much larger than the quantity required to form the crater wall. The inference is that the level of the surface has been slightly raised even at a great distance from the place of the splash. Figs. 7, 8, and 9 of Series VI themselves confirm the impression of the undisturbed flatness of the surface at even a small distance from the splash.
(2) THE SPLASH OF A SMOOTH SPHERE.
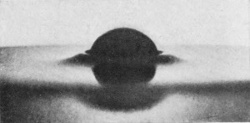
The reader who has been sufficiently interested to make for himself the simple experiment suggested at the beginning of this chapter, will have already realized that the splash of a smooth sphere is totally different from that of a rough one. The photographs [pg 90] of Series IX show that the difference is quite pronounced from the first instant of contact. In this series the sphere was of polished stone 3·2 cm. in diameter and fell 14 cm. The scale of magnification is 3/4. The second figure shows that the liquid, instead of being driven away from the surface as was the case with a rough sphere, now rises up in a thin, closely-fitting sheath which (see Fig. 3) completely envelops the sphere even before its summit has reached the water-level. Figs. 4 and 5 show the comparatively insignificant column that remains to mark the spot where the sphere has entered. Fig. 6 was the result of a lucky accident, which left the sphere rough on the right-hand side, smooth on the left. Nothing could show better than this photograph the essential difference between the two splashes.
SERIES VIII
Rough sphere. Splashes viewed below the surface.
The bursting of the bubble.
| 1 0·055 sec. |
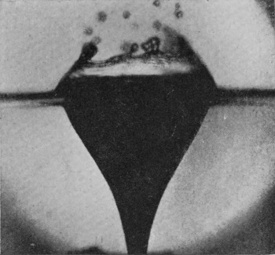 |
From a splash into Petroleum
24·5 cm. fall.
| 2 0·060 sec. |
 |
3 0·064 sec. |
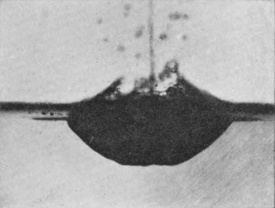 |
From a splash into Petroleum
32 cm. fall.
| 4 0·070 sec. |
 |
5 0·082 sec. |
 |
The reader's attention is directed to the remarkably deep furrows which characterize the whole sheath in Fig. 3 and the left-hand (smooth splash) part in Fig. 5. About these furrows we shall have something to say later.
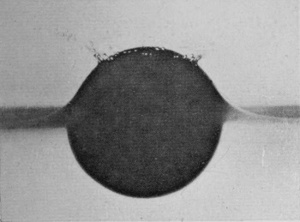
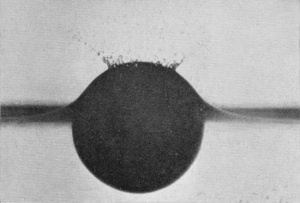
A better idea of the extreme thinness of the enveloping sheath is obtained when the illumination is from behind as in Series X, in which the sphere was of highly polished serpentine stone 2·57 cm. (or just over 1 inch) in diameter, the fall being 14 cm. (or not quite 6 inches).
SERIES IX
The "sheath" splash of a smooth sphere.
|
|
||||||||||
|
|||||||||||
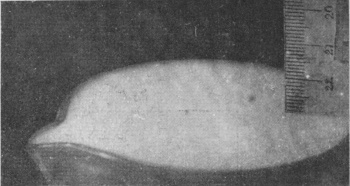
Examination of either Series IX or Series X shows that with the smooth sphere as with the rough the amount of water lifted above the surface in the [pg 92] immediate neighbourhood of the splash is much less than the whole volume displaced, so that we are again driven to the conclusion that the surface at even a considerable distance must be bodily lifted without its flatness being sensibly disturbed. This conclusion was confirmed by a direct experiment. The not very wide vessel of Fig. A was taken and filled brimful with milk, and the lower edge of a card millimetre scale was placed just in contact with the liquid surface at one side. The reader should notice that the liquid is not quite up to the level of the spout on the right-hand side of this figure. Then the sphere was dropped in and the photograph of Fig. B was taken when the sphere was about two-thirds immersed. The rise at the edge of the scale is about 3 millimetres, and there is an apparently equal rise at the spout, where, however, the surface appears quite flat.
 |
 |
|
Fig. A |
Fig. B |
It seems probable, then, that whenever a stone is thrown into a lake the impulse accompanying its entry travels with the velocity of a compressional wave (i.e. with the velocity of sound) through the [pg 94] liquid, and is therefore almost instantly felt and produces a minute rise of level even in remote parts of the lake long before the arrival of any ripple or surface disturbance.
SERIES X
Polished serpentine sphere falling 14 cm. into water.
| 1 0·003 sec. |
 |
2 0·006 sec. |
 |
| 3 0·008 sec. |
 |
4 0·011 sec. |
 |
| 5 0·013 sec. |
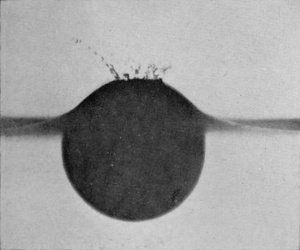 |
6 0·014 sec. |
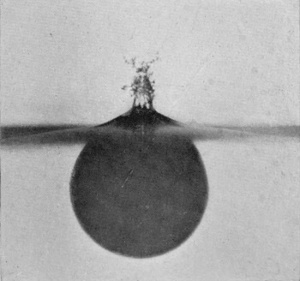 |
It may here be observed that whether the sphere be rough or smooth, its size makes little or no difference in the character of the splash, within a range of diameter from 12 to 32 millimetres—i.e. from about 1/2 inch to about 1-1/3 inches. No doubt with a very large sphere, taking a long time to enter, the splash would be controlled more by gravity than by surface-tension, but so long as the sphere is within the limits mentioned this is not the case unless the height of fall be made very small indeed.
CHAPTER VIII
THE TRANSITION FROM THE SMOOTH OR "SHEATH" SPLASH TO THE ROUGH OR"BASKET" SPLASH
THE INFLUENCE OF VELOCITY.
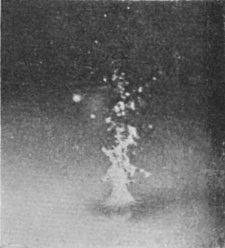
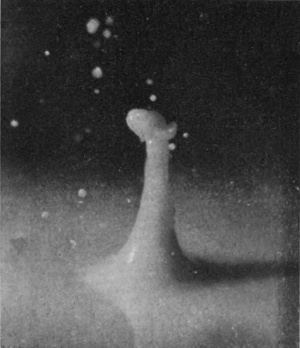
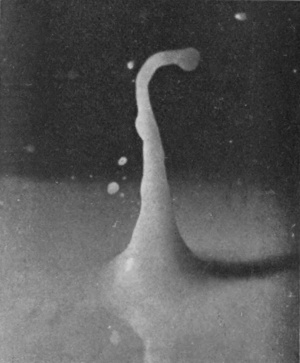
If we gradually increase the velocity with which a well-polished sphere enters the liquid we find that there is a gradual transition from the silent "smooth" or "sheath" splash taking down no air and giving rise to only an insignificant column, to the noisy, "rough," "basket" splash taking down much air and throwing up a tall and conspicuous jet. Thus in the fourth figure of Series XI, in which the height of fall has been increased from 15 to 60 cm. (i.e. from 6 inches to 2 feet), the sphere being of polished ivory, we see that the enveloping sheath has in many places broken away from the surface before the summit has been covered. It is well known that a sphere moving through a liquid pushes away the liquid in front of it, which flowing round closes in at the back of the sphere.
[pg 96] Although the surface round the column of Fig. 6 is still very flat, the liquid just below it must be streaming inwards,[G] as is indicated by the radial striæ. To the meeting of these converging streams we must attribute the large access of liquid that is forced up into the column, whose subsequent toppling into drops is accompanied by the curious, characteristic, lop-sided curvature of the later figures.
SERIES XI
Polished ivory sphere, 1·9 centim. in diameter, falling 60 cm. into water mixed with milk.
| 1 | 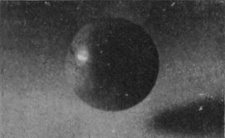 |
2 T = 0 |
 |
3 | 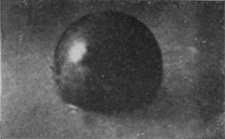 |
| 4 0·002 sec. |
 |
5 | 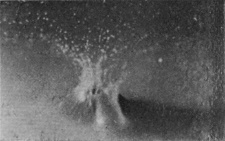 |
6 0·004 sec. |
 |
| 7 0·031 sec. |
 |
8 0·045 sec. |
 |
| 9 0·062 sec. |
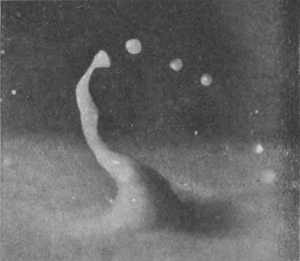 |
[pg 98] Series XII shows how even with a very highly polished metal sphere falling into water from the still greater height of 100 cm. the characteristic sheath of the "smooth" splash is no longer so closely fitting even at an early stage, but is beginning to resemble the earlier stages of the basket-shaped crater of the "rough" splash; yet no air was taken down at this height.
The transition was also watched by means of photographs taken below the water-line.
It may be well here to guard the reader against a possible misconception. The curved outline of the liquid in these photographs does not represent the path followed by the particles. Each particle must have travelled in a nearly straight line from the moment it left the surface of the sphere, and must still be moving upwards and outwards. Gravity has not had time to produce any sensible displacement. This applies also to the curved outlines in many other early figures.
INFLUENCE OF THE CONDITION OF THE SURFACE.
By very careful rubbing of such a polished, steel sphere, it was found possible to increase the height of fall to 162·5 cm. (well over 5 feet) and yet to secure a perfectly "airless," "smooth" splash. But the equilibrium of the splash, if I may use the phrase, is, at this high velocity of entry (564 cm. per sec., or about 18 feet per sec.), very unstable, and was found to depend on minute differences in the condition of the surface. [pg 100] How minute this difference may be, which yet makes the whole difference in the character of the splash, may be gathered from the following extract from the original paper:—
SERIES XII
Smooth sphere of polished serpentine falling 100 centim. into water. Scale 3/4.
| 1 T = 0 |
 |
| 2 0·001 sec. |
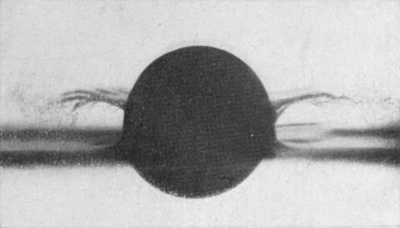 |
| 3 0·002 sec. |
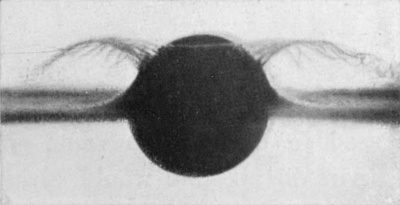 |
"A polished steel sphere 15·9 cm. in diameter was found (by naked-eye observation) to give an airless splash when falling into water from a height of 132·5 cm.; at 137·5 cm., there was much air taken down. This observation at 137·5 cm. was repeated three times, observer C. doing the polishing. Then observer W. polished, and the splash was first nearly airless and then quite airless. Then, by persevering in the rubbing, the height of fall was gradually raised to 162·5 cm., and a perfectly airless splash was secured, and even at 172·5 cm. the record was 'very little air indeed.'
"Again, a polished marble sphere 2·57 cm. in diameter falling into water from a height of 112 cm. was found to take down 'much air' when rubbed with a certain clean handkerchief A, and 'none at all, or only very little,' when rubbed with clean handkerchief B. This result was confirmed four times with B and five with A. These handkerchiefs were subsequently examined under the microscope, but were found to be extremely similar, and the cause of the difference remained for the time beyond conjecture.
"On another occasion, of two similar nickel-plated steel spheres, each 19 millimetres in diameter, and each treated in exactly the same way, falling 22 cm. into paraffin oil, one would always take down much air and the other little or none, and again [pg 101] microscopic examination showed only a very slight difference in the surfaces."
By wetting the surface of a smooth sphere we can always convert a smooth or "sheath" splash into a rough or "basket" splash. Thus when the ivory sphere (which when dry and well-polished gave, with a fall of 60 cm., the splash of Series XI, p. 97), was allowed to fall wet into the liquid, all other circumstances remaining the same, the splash of Series XIII, p. 103, was obtained, which is entirely different from the first. The wetting was effected by dipping the sphere into the bowl of milky water into which it was to fall, and then shaking off as much as possible of the adherent liquid, but in all cases the splash quickly became unsymmetrical, probably through the liquid, during the fall, drifting to one side of the sphere.
INFLUENCE OF THE NATURE OF THE LIQUID.
The nature of the liquid employed has a great influence in determining whether at a given height the splash shall be "rough" or "smooth."
Thus with paraffin oil the maximum height that could be reached with an airless splash with highly polished nickel-plated spheres, well rubbed on a selvyt cloth, was found to be only 24·7 cm. (about 10 inches), but, with water, a fall of 160 cm. (over 5 feet) could be reached. The paraffin oil used in these experiments had, at a temperature of 12°·5 centigrade, a specific gravity ·840 and a surface-tension about ·39 of that of water. Since only a small increase of height was required with this liquid to make a smooth sphere give [pg 102] the same splash as a rough one, this liquid was found much more convenient than water in investigating the transition.
When water is made more viscid by the gradual addition of glycerine,[H] the surface-tension and the specific gravity are but little altered though the viscosity is steadily and sensibly increased. An admixture of two parts of glycerine to fifty-one of water produced no perceptible change in the splashes observed. When the glycerine was increased to six volumes in fifty-one of water, though this made the viscosity half as great again, the change was noticeable but still slight, the chief difference being, with a smooth sphere, the greater salience of the ribs or flutings in some of the earlier stages of the glycerine splash, and the much greater reluctance of the subsequent jets to topple into droplets. This latter feature is well seen in the first figure on page 105, showing the entry of a smooth sphere of polished serpentine stone into this glycerine mixture from a height of 50 cm.
SERIES XIII
Splash of a smooth wet sphere.
| 1 T = 0 |
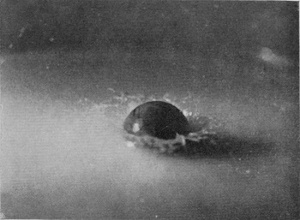 |
| 2 0·003 sec. |
 |
| 3 0·015 sec. |
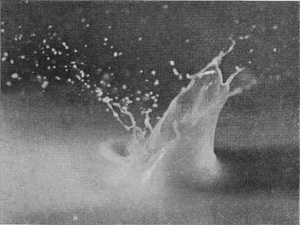 |
4 0·037 sec. |
 |
With pure glycerine, which is much more viscous, the splash of the same polished serpentine sphere falling from 75 cm. (about 2-1/2 feet), is shown in Series XIV. In the original photographs the radial furrows on the right-hand side of Fig. 2 are very pronounced, and even in Fig. 1 the fluting of the film is seen to be already well developed on the left-hand side; but [pg 104] these details have proved rather too delicate for reproduction in the plate. Two photographs taken of stage 2 had each of them an isolated jet, owing probably to the fact that when working with so sticky a liquid it was difficult to avoid contaminating the cloth on which the sphere was each time repolished after washing in water, with the result that the spheres behaved as if locally rough. The relatively great length and height of this jet brings out well the part played by viscosity, both in delaying segmentation into droplets and also in hindering the flow of the rest of the liquid sheath which has remained in contact with the sphere.
With a rough sphere falling into pure glycerine from the same height of 75 cm., except for an occasional jet that may escape as in Fig. 4 of Series XV, the proceedings are uneventful, as a glance at the series will show. With the same height of fall into water we should have had an exquisite crater fringed with a multitude of fine jets, and ultimately closing to form a bubble. We thus see how little play is given to the action of the surface-tension in a very viscous liquid.
THE INFLUENCE OF TEMPERATURE.
It was found that if a polished sphere was heated in boiling water, quickly rubbed dry, and let fall while still hot, a very marked difference was produced. With the sphere hot, the height of fall can be much increased before the splash becomes "rough." Thus with paraffin oil, the height with a nickel-plated sphere rose from 22·2 cm. to 29·3 cm., and with water from 157 cm. to 234 cm.
THE REMARKABLE INFLUENCE OF A FLAME HELD NEAR THE LIQUID, AND TRAVERSED BY THE SPHERE IN ITS FALL.
In our search for the explanation of the difference between the rough and the smooth splash, it occurred to us to let the smooth sphere drop through a flame held near the liquid, and the result was very remarkable. With paraffin oil (and the sphere hot) the airless height now rose from 29·3 cm. to 45·3 cm., and with water and a cold sphere, it rose from 157 cm. to over 258 cm., which was the greatest height that the laboratory would permit. Either the luminous flame of a bat's-wing burner or the flame of a Bunsen burner held nearly horizontal produces the effect, provided the flame is held near enough to the surface of the liquid, and it is a very striking experiment to let the polished sphere fall several times from a height which gives a large volume of bubbles rising with much noise to the surface, and then to let it fall through the flame, and to observe the complete [pg 107] change in the phenomenon. On a sphere already roughened the flame has no observable effect.
THE SUPPOSITION OF ELECTRIFICATION TESTED AND REJECTED.
The behaviour with a flame led at first to the supposition that we had to deal with an electrical phenomenon, for a flame would certainly discharge completely any electrified sphere passing through it, and it appeared reasonable to suppose that the sphere might become electrified by friction with the air through which it fell.
It required a long series of experiments, into the details of which I need not now ask my readers to enter, to prove that this tempting explanation was untenable, and that there was no reason to believe that electrification had anything to do with the matter.
EXPERIMENTS IN VACUO.
It remained to examine what part was played by the air in the whole transaction. This could only be settled by removing the air and letting the spheres, whether rough or smooth, fall through a vacuum into the liquid, or rather through a space occupied only by the vapour of the liquid in use.
Instantaneous photographs obtained under these conditions showed that the presence of the air has no material influence on the early course of the splash, and that a sphere which gives a "smooth" splash in air will give a "smooth" splash in vacuo, while if the splash is "rough" in air, it will also be "rough" in vacuo.
FOOTNOTES:
[G] Some useful information about the internal flow of the liquid was obtained by the device of letting the sphere descend between two slowly ascending streams of very minute bubbles liberated by electrolysis at two electrodes placed in the liquid. These streams, initially straight and vertical, were displaced and distorted as the sphere passed near them and afforded a measure of the displacement of the fluid at different points. For details see Phil. Trans. Roy. Soc., Vol. 194, p. 178 (1900).
[H] Glycerine was found to be a rather treacherous liquid, requiring special precautions for which the reader who desires details is referred to the original memoir. Phil. Trans. Roy. Soc., Series A, 1900. Vol. 194, p. 198.
CHAPTER IX
THE EXPLANATION OF THE CAUSE OF DIFFERENCE BETWEEN THE TWO SPLASHES
I have some hope that, by the enumeration of the many surprising and puzzling facts mentioned in the last chapter, I may have succeeded in producing in the mind of my reader some sympathy with the state of perplexity of Mr. Cole and myself when, after four years of experimenting, we found ourselves still unable to answer the question, "Why does the rough sphere make one kind of splash, the smooth sphere another kind?"
By reflecting, however, on all the facts at our disposal, we were at last led to what seems to be an entirely satisfactory explanation, and one moreover which we were able to test by further experiment.
This explanation may be stated as follows:—
When a sphere, either rough or smooth, first strikes the liquid, there is an impulsive pressure between the two, and the column of liquid lying vertically below the elementary area of first contact is compressed. For very rapid displacements the liquid on account of its viscosity behaves like a solid. In the case of a solid rod we know that the head would be somewhat flattened out by a similar blow, and a wave of [pg 109] compression would travel down it; to this flattening or broadening out of the head of the column corresponds the great outward radial velocity, tangential to the surface, initiated in the liquid, of which we have abundant evidence in many of the photographs. (See pp. 75, 87, and 99.)
Into this outward-flowing sheath the sphere descends, and since each successive zone of surface which enters is more nearly parallel to the direction of motion of the sphere, the displacement of liquid is most rapid at the lowest point, from the neighbourhood of which fresh liquid is supplied to flow along the surface. Whether the rising sheath shall leave the surface of the sphere, or shall follow it, depends upon the efficiency of the adhesion to the sphere. If the sphere is smooth and clean, the molecular forces of cohesion will guide the nearest layers of the advancing edge of the sheath, and will thus cause the initial flow to be along the surface of the sphere.
To pull any portion of the advancing liquid out of its rectilinear path the sphere must have rigidity. If the advancing liquid meets loosely attached particles, e.g. of dust, these will constitute places of departure from the surface of the sphere; the dust will be swept away by the momentum of the liquid which, being no longer in contact with the sphere, perseveres in its rectilinear motion. If the dust particles are few and far between, the cohesion of the neighbouring liquid will bring back the deserting parts, but if the places of departure are many, then the momentum of the deserters will prevail. Thus at every instant [pg 110] there is a struggle between the momentum of the advancing edge of the sheath and the cohesion of the sphere; the greater the height of fall the greater will be the momentum of the rising liquid, and the less likely is the cohesion to prevail, and the presence or absence of dust particles may determine the issue of the struggle.
Roughness of the surface will be equally efficient in causing the liquid to leave the sphere. For the momentum will readily carry the liquid past the mouth of any cavities (see Fig. 20), into which it can only enter with a very sharp curvature of its path. It is to be observed that the surface-tension of the air-liquid surface of the sheath will act at all times in favour of the cohesion of the sphere, and even if the film has left the sphere the surface-tension will tend to make it close in again, but we should not be right in attributing much importance to this capillary pressure which, with finite curvatures, is a force of a lower order of magnitude than the cohesion, and, as the photographs now to be shown will clearly show, is incompetent to produce the effects observed.
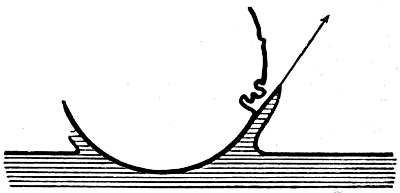
Fig. 20
Having arrived at this general explanation, we proceeded to test it.
EXPERIMENTS ON THE INFLUENCE OF DUST.
In the first place, to test the influence of dust, the experiment was made of deliberately dusting the [pg 111] surface of the sphere. For this purpose a highly polished nickelled sphere was held in a pair of crucible tongs by an electrified person standing on an insulating stool, and by him presented to any dusty object that stood or could be brought within reach. Particles of dust soon settled on the electrified sphere, which was then carefully placed on the dropping ring with the dusty side lowest. The liquid used was paraffin oil, and the height of fall was 31·7 cm., at which this sphere when not dusted gave always a quite airless splash. When dusted an enormous bubble of air was carried down on each occasion. Although the sphere when laid on the dropping ring must have completely lost the electrical charge, yet it seemed worth while to go through the same electrifying process without dusting. The result showed that no change was produced. In order to see how far the influence of dust would go, the height of fall was now reduced, and it was found that with sphere (1) a fall of 17·1 cm. gave a perfectly rough splash when the surface was visibly dimmed with fine dust, and with a second similar sphere a fall of 16·7 cm. availed. If the surface was only slightly dusty, then at these low heights the splash remained "smooth."
It then occurred to us to try the effect of partial or local dusting, for we had already found by experimenting with a marked sphere that the method of dropping did not impart any appreciable rotation to the sphere, which reached the liquid in the attitude with which it started from the dropping ring. [pg 112] Accordingly, after dusting the sphere in the manner already described, the dust was carefully rubbed away from all but certain parts whose position was recorded. The experiments were very successful, and the results are shown on page 113. The liquid used was water, and the sphere was of polished serpentine, 2·57 centim. in diameter, falling 14 centim.
In Fig. 1 of Series XVI the sphere was dusted on the right-hand side, and a "sound of splash" was recorded. On the left side we see that there is no disturbance of the "smooth splash"; on the right is a "pocket" of air such as was obtained by accident in Series IX, Fig. 6 (see p. 91). The point of departure at which the liquid left the sphere is well marked, and a tangent from this point passes through the outermost conspicuous droplets that must have been projected from it.
In Fig. 2 the sphere was dusted at the top and on the right-hand side, but not much more than half-way down, and the configuration corresponds entirely to the facts. Here again a tangent from the well-marked drops on the right-hand side leads very nearly to the place of departure from the surface of the sphere.
In Fig. 3 the sphere was dusted near the bottom only. The appearance on the left-hand side seems to show that the liquid has, after leaving the sphere, again been brought within reach. This recovery at an early stage is explained by reference to photographs of Series VI (p. 81) of the splash of a rough sphere, which show that even the rough sphere is soon wetted for some distance up the sides, by the [pg 114] gradual passage of the sphere into the divergently flowing cone of liquid which surrounds the lower part. When the liquid again touches a polished part the film will be again guided up it in the manner already explained.
SERIES XVI
Spheres dusted at one side.
| 1 | 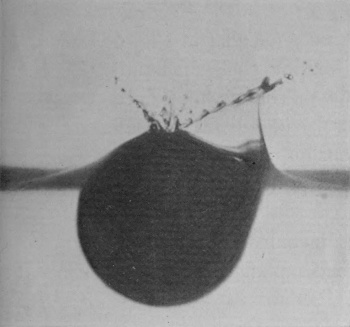 |
2 | 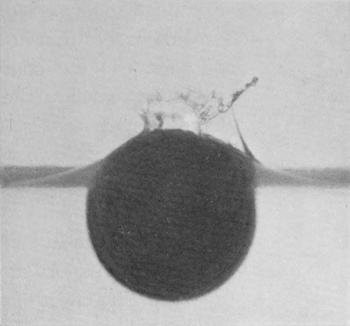 |
| 3 | 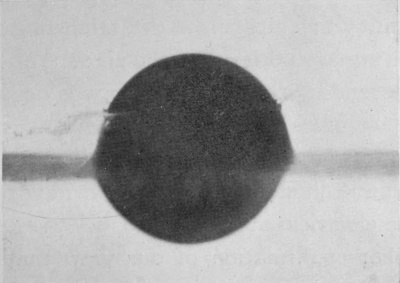 |
We observe that in Figs. 1 and 2 (as also in Fig. 6 of page 91) the continuous film or shell of liquid no longer reaches the outermost droplets that once have been at its edge. It must evidently have been pulled in by its own surface-tension, which of course will cease to exercise any inward pull on a drop that has once separated.
The influence of dust, thus incontestably proved, seems also to afford a satisfactory explanation of—
(1) The effect of a flame.
(2) The effect of heating.
(3) The variable and uncertain effects of electrification.
For, (1), we may suppose that the flame burns off minute particles of dust; (2), we know from Aitken's experiments[I] that dust from the atmosphere will not settle on a surface hotter than the air; (3) an electrified sphere descending through the air would attract dust to its surface unless it happened, as well might happen, that the air round about it, with its contained dust, had become itself similarly charged through the working of the electrical machine.
In further confirmation of our view that the leading clue to the explanation of the motion is the struggle between the adhesion of the rigid sphere and [pg 115] the tangential momentum of the liquid, we may cite the following points:—
A liquid sphere makes a "rough" splash, and the photographs obtained show that the lower part of the in-falling drop is swept away by the tangential flow, while the upper part is still undistorted. Here we have cohesion but no rigidity.
Also we find that the "rough" splash is obtained by any process which gives a non-rigid surface to the sphere. Thus the splash made by a marble freshly roughened by sand-papering, or by grinding between two files and let fall from the very small height of 7·5 cm., can be practically controlled by attending to the condition of the surface. If the surface is quite dry and still covered with the fine powder resulting from the process of roughening, the splash is "rough," and a great bubble of air is taken down. But if this coat of powder, which has neither cohesion nor shearing strength, be removed by rubbing, the splash (under this low velocity) is "smooth." Again, a marble freshly sand-papered and covered with the resulting powder, if let fall from 12 or 15 cm., gives a rough splash. The same marble picked out of the liquid and very quickly dropped in again from the same height, will give again a rough splash. Here the liquid film is thick and "shearable." But if the same sphere be allowed to drain or be lightly wiped, the splash will be smooth. We may conjecture that in this case enough fluid is left to fill up the interstices, but that the coat is not thick enough to shear easily. If, however, the sphere be thoroughly dried, the splash [pg 116] becomes "rough" again. This gives us the explanation of the facts already recorded in respect of the splash of a wet sphere. This splash was always irregular; the liquid drifted to one side where it would shear, while it disappeared from the other or became there too thin to shear, though sufficient to fill up crevices.
EXPLANATION OF THE RIBS OR FLUTINGS IN THE SPLASH OF A SMOOTH SPHERE.
The fact thus established experimentally, that the surface of a smooth sphere must be rigid if the film is to envelop it closely, suggests also a satisfactory explanation of the flutings. For we know from other researches on the motion of liquids,[J] that a layer of liquid actually in contact with a solid can have no motion relative to the solid, but must move with it. Thus in the film or sheath which rises over and envelops the sphere, the layer of liquid next to the solid must be moving downwards with it, while the outermost layers at least are moving upwards; thus there must be a strong viscous shear in the film impeding its rise. If by any fortuitous oscillation a radial rib arises, this will be a channel in which the liquid, being farther from the surface, will be less affected by the viscous drag; it will therefore be a channel of more rapid flow and diminished pressure, into which, therefore, the neighbouring liquid will be forced from either side. Thus a rib once formed is in stable equilibrium, and will correspond to a jet at [pg 117] the edge of the rim. This explains the persistence of the ribs when once established, and we may attribute their regular distribution to the fact that they first originate in the spontaneous segmentation of the annular rim at the edge of the advancing sheath. This explanation quite accords with the appearance of such figures as Fig. 6 of page 91 and Figs. 1 and 2 of page 113, in which, firstly, we see that the flutings are absent from that part of the sheath which has left the sphere, and, secondly, we see how much higher in every case the continuous film has risen in that part which has left the sphere than in the part which has clung to it, and has been hindered by the viscous drag. Especially is this the case in Fig. 2, Series XIV (p. 105), where the liquid was pure glycerine. The effect of the viscous drag is, in fact, most marked in the most viscous liquid, and it is also in the viscous liquid that the ribs are most strongly marked.
INFLUENCE OF THE NATURE OF THE LIQUID EXPLAINED.
Finally, in confirmation of our explanation, we have the fact that with a liquid of small density and surface-tension, such as paraffin oil, a much smaller velocity of impact with a highly polished sphere suffices to give a "rough" splash than with water, a liquid of greater density and surface-tension, the reason being without doubt that the tangential velocity given by the impact is greater with the lighter liquid, as, indeed, is proved to be the case by the greater height to which the surrounding sheath is thrown up. The surface-tension also being smaller, the less is the abatement of velocity on account of work done in extending the surface.
FOOTNOTES:
[I] See Nature, vol. xxix., January 31, 1884.
[J] See Whetham on "The Alleged Slipping at the Boundary of a Liquid in Motion." Phil. Trans. Roy. Soc., Vol. 181 (1890).
CHAPTER X
CONCLUSION
We have now reached the end of the story, as far at least as I am able to tell it. But there is certainly more to be found out. No one has yet examined what happens when a rough sphere enters a liquid with a very high velocity. That the motion set up must differ from that at a low velocity is apparent to any one who has thrown stones from a low bridge into deep water below. The stone that is thrown with a great velocity makes neither quite the same sound nor the same kind of splash as a slow-falling stone, and though in the light of our present knowledge we may conjecture the kind of difference to be expected, yet experience has taught me that the subject is so full of unexpected turns that it is better to wait for the photographic record than to speculate without it.
It would be an immense convenience, as was suggested in the first chapter, if we could use a kinematograph and watch such a splash in broad daylight, without the troublesome necessity of providing darkness and an electric spark. But the difficulties of contriving an exposure of the whole lens short enough [pg 119] to prevent blurring, either from the motion of the object, or from that of the rapidly-shifting sensitive film, are very great, and any one who may be able to overcome them satisfactorily, will find a multitude of applications awaiting his invention.
But even were the photographic record complete, what does it amount to? All that we have done has been merely to follow the rapid changes of form that take place in the bounding surface of the liquid. The interior particles of the liquid itself have remained invisible to us. But it is precisely the motion of these particles that the student of hydrodynamics desires to be able to trace. His study is so difficult that even in the apparently simple case of the gently-undulating surface of deep water, the reasoning necessary to discover the real path of any particle can at present only be followed by the highly-trained mathematician. In other and more complicated cases such as are exemplified by the sudden disturbances that we have studied, any definite information that can be obtained, even as to the motion of the surface, may afford a clue to the solution of important questions; and I have been encouraged to hope that the observations here recorded may serve as a useful basis of experimental fact in a confessedly difficult subject.
To take a single illustration of a possible application in an unexpected quarter, I would invite the attention of the reader to the two photographs in the frontispiece, which exhibit the splash of a projectile on striking the steel armour-plate of a battleship. These are ordinary photographs taken after the plate [pg 120] had been used as a target. They represent the side on which the projectile has entered. In one picture the projectile is still seen embedded in the plate.
No one looking at these photographs can fail to be struck with the close resemblance to some of the splashes that we have studied. There is the same slight upheaval of the neighbouring surface, the same crater, with the same curled lip, leading to the inference that under the immense and suddenly applied pressure, the steel has behaved like a liquid.
Such flow of metals under great pressure is familiar enough to mechanical engineers, but what I desire to suggest is, that from a study of the motions set up in a liquid in an analogous case, it may be possible to deduce information about the distribution of internal stress, which may apply also to a solid, and may thus lead to improvements in the construction of a plate that is intended to resist penetration.
CHAPTER XI
(SUPPLEMENTARY)
A NEW PHENOMENON THAT APPEARS WITH AN INCREASE IN THE VELOCITY OF ENTRY OF A ROUGH SPHERE
A slight delay in the passage of this book through the press has enabled me to obtain some of the missing information referred to in the opening paragraph of the last chapter.
If any reader who may have been persuaded to try for himself the simple experiment mentioned at the beginning of Chapter VII, will extend his observations by increasing the height of fall of the roughened marble to 4 or 5 feet (say to 140 centim.), he will find that while, as before, much air is still carried down, there is nevertheless, now, no rebounding jet projected high into the air, such as is invariably seen with the lower fall of 2 feet (60 centim.), and he will notice a curious "seething" appearance at the surface.[K] Thinking that this appearance which the naked eye detects must be due to an entanglement of the rising jet with the bubble, which entanglement was likely to produce confused motions that could not be profitably studied, I had not till now been sufficiently curious to examine what really happened. But certain recent observations of the persistence with which the seething motion again and again re[pg 122]curred when a stone was dropped or thrown into a river, led me to suspect that something required investigation. I was, however, quite unprepared to find the remarkable change of procedure that is revealed by the following series of photographs (Series XVII), in the taking of which I owe much to the kind and skilful assistance of Dr. Bryan. The earlier figures show the very rapid rise of the crater and its closing as a bubble much before the entrapped column of air divides. Before the division takes place, the liquid now flowing in from all sides closes over the upper end of the long air-tube, separates it from the air outside, and forms a downward jet which shoots down the middle of the air-tube in pursuit of the sphere. The first formation of this jet is not easy to observe, because the view is obscured by much splashing and turbulent vortical motion resulting apparently from the collision of the streams that converge from all sides on the axis of the air-tube at its upper end. Thus in Fig. 5 the jet is not yet well established, or at least not easily discerned; but in Fig. 6 the turbulence has cleared away from the upper part, and from this stage onwards the jet is well seen in all the figures, and it persists long after the segmentation of the air column has taken place. The reader must not suppose that this jet is a mere falling of the water under the action of gravity, for the rapidity with which it advances is far greater than could be accounted for in this way; indeed, as the "times" show, the effect of gravity during the establishment of the jet is insignificant.
SERIES XVII
Rough sphere falling 140 cm. into water. Scale 2/3.
| 1 0·006 sec. |
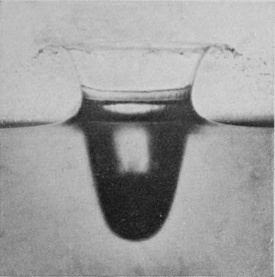 |
2 0·008 sec. |
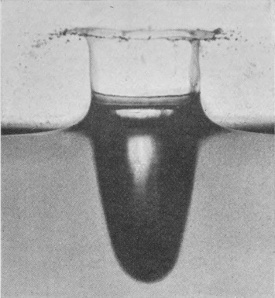 |
| 3 0·015 sec. |
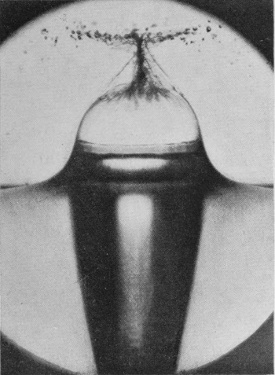 |
4 0·021 sec. |
 |
| 5 0·038 sec. |
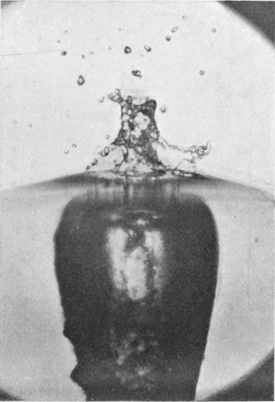 |
[pg 124] The segmentation of the air column appears to be independent of the jet; but some photographs, such as Fig. 7, show the jet striking the side and breaking into the surrounding liquid with a great accompaniment of "air-dust."
SERIES XVII—(continued)
| 6 0·043 sec. |
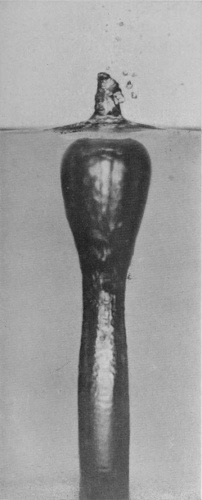 |
7 0·052 sec. |
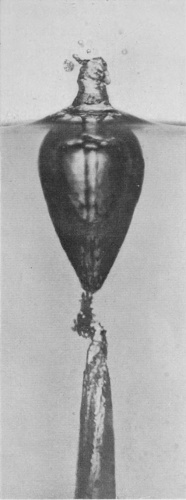 |
N.B.—Each of these figures is made up from two photographs; one of the upper and one of the lower portion taken from different splashes, but with the same "timing."
[pg 126] The reader will observe that after division of the air-tube has taken place, say from Fig. 9 onwards, the water entering the jet at the top and coming out again at the bottom must circulate as in a vortex ring, part of the core of which is filled with the air surrounding the jet.
It is also to be observed that after the establishment of the jet, there is a steady increase in the size of the heap above the surface; but it is not easy in any given photograph to say how much of this protuberance is air and how much is water. An examination of Figs. 7, 8, and 9 shows that the place of origin of the jet is gradually lifted above the level of the free surface.
That the jet we now see should be directed downwards rather than upwards may, I think, be explained in a general way as follows:—The great initial momentum of the sphere causes it to continue in rapid motion after the bubble has closed, thus the sphere acts as a sort of piston, which by increasing the length of the air-tube diminishes the pressure in it and so sucks in the bubble, which is driven down by the greater atmospheric pressure above. The converging horizontal inflow near the mouth of the air-tube cannot, of course, produce the downward-directed jet without an equal and opposite generation of momentum upwards; but this is now expended, not in producing a similar upward jet, but in balancing the excess of atmospheric pressure. The reaction, in fact, to the projection of the jet downwards, is the force which holds up and slowly raises the roof of the long air-shaft.
SERIES XVII—(continued)
| 8 0·057 sec. |
 |
9 0·063 sec. |
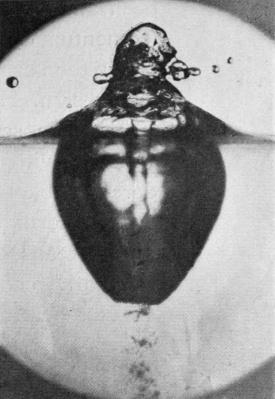 |
| 10 0·073 sec. |
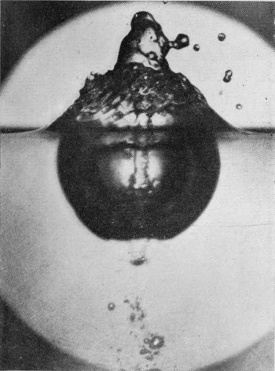 |
11 0·089 sec. |
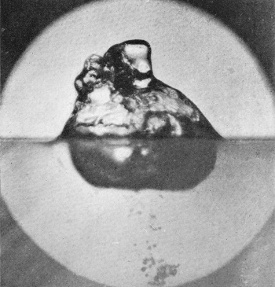 |
[pg 128] When, as in the last figure of Series VI, p. 85, we saw the upward-directed jet, then also there must have been an equal and opposite generation of downward momentum distributed in some way through the liquid below the basin, of which, however, there could be no visible sign. Hence we see that the present downward jet is, in a sense, not a new phenomenon, but one which, having existed unnoticed before, is now rendered visible to us by reason of its being produced in air instead of in water.
By means of a hole bored through the ceiling of the dark room, the fall was then increased to 281 centim. (just over 9 feet). The very beautiful earlier stages of the splash at this height are shown in Series XVIII. Fig. 4 shows very well the internal splashing at the top of the air-column which accompanies the initiation of the jet. Some later photographs taken at this height (not yet quite presentable) show the jet passing right down the narrow neck of air-tube and probably striking the top of the sphere, the descent of which must thus be liable to a curious irregularity.
A further increase of the height of fall to 686 centim. (22-1/2 feet) was found to produce but little change in the phenomena.
SERIES XVIII
Early stages of the splash of a rough sphere (diam. 1·5 centim.) falling 281 centim. (about 9 feet) into water.
| 1 T = 0 |
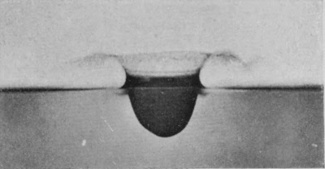 |
| 2 0·003 sec. |
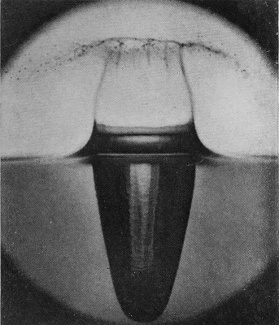 |
3 0·005 sec. |
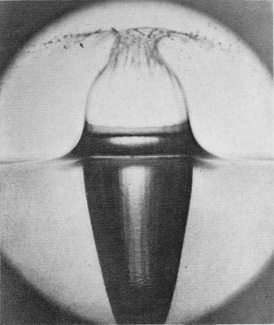 |
| 4 | 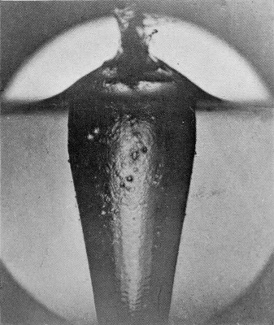 |
FOOTNOTES:
[K] I can recommend any reader who is not afraid of being late for breakfast to keep a bag of marbles in his bath-room.
PRINTED BY
WILLIAM BRENDON AND SON, LTD
PLYMOUTH