- ^ Hafele, J.; Keating, R. (July 14, 1972). "Around the world atomic clocks:predicted relativistic time gains". Science 177 (4044): 166-168. doi:10.1126/science.177.4044.166. Retrieved on 2006-09-18.
- ^ Hafele, J.; Keating, R. (July 14 1972). "Around the world atomic clocks:observed relativistic time gains". Science 177 (4044): 168-170. doi:10.1126/science.177.4044.168. Retrieved on 2006-09-18.
- ^ A. G. Kelly,Reliability of Relativistic Effect Tests on Airborne Clocks, Monograph No.3 Feb.1996, The Institution of Engineers of Ireland, ISBN 1-898012-22-9
- ^ Louis Essen, Electron. Wireless World 94 (1988) 238.
- ^ : Feedback : National Physical Laboratory
- ^ Deines, "Uncompensated relativity effects for a ground-based GPSA receiver", Position Location and Navigation Symposium, 1992. Record. '500 Years After Columbus - Navigation Challenges of Tomorrow'. IEEE PLANS '92.

|
The Hafele–Keating experiment was a test of the theory of relativity. In October of 1971, J. C. Hafele and Richard E. Keating took four cesium-beam atomic clocks aboard commercial airliners and flew twice around the world, first eastward, then westward, and compared the clocks against those of the United States Naval Observatory. Overview According to special relativity, the speed of a clock is greatest according to an observer who is not in motion with respect to the clock. In a frame of reference in which the clock is not at rest, the clock runs slower, and the effect is proportional to the square of the velocity. In a frame of reference at rest with respect to the center of the earth, the clock aboard the plane moving eastward, in the direction of the earth's rotation, is moving faster than a clock that remains on the ground, while the clock aboard the plane moving westward, against the earth's rotation, is moving slower. According to general relativity, another effect comes into play: the slight increase in gravitational potential due to altitude that speeds the clocks back up. Since the aircraft are flying at roughly the same altitude in both directions, this effect is more "constant" between the two clocks, but nevertheless it causes a difference in comparison to the clock on the ground. The results were published in Science in 1972:[1][2]
The published outcome of the experiment was consistent with special relativity, and the observed time gains and losses were reportedly different from zero to a high degree of confidence. That result was contested by Dr. A. G. Kelly who examined the raw data: according to him, the final published outcome had to be averaged in a biased way in order to claim such a high precision.[3] Also, Louis Essen, the inventor of the atomic clock, published an article in which he discussed the (in his opinion) inadequate accuracy of the experiment.[4]; however, neither of these publications are in peer-reviewed sources. One notable approximate repetition of the original experiment took place on the 25th anniversary of the original experiment, using more precise atomic clocks, and the results were verified to a higher degree of accuracy.[5]. Nowadays such relativistic effects have been incorporated into the calculations used for the GPS system[6]. Equations The equations and effects involved in the experiment are: Total time dilation Τ = Δτv + Δτg + Δτs Velocity Gravitation Sagnac effect Where h = height, v = velocity, ω = Earth's rotation and τ represents the duration/distance of a section of the flight. The effects are summed over the entire flight, since the parameters will change with time. References
See also * Twin paradox Retrieved from "http://en.wikipedia.org/" |
|
||||||||||||||||||||||||
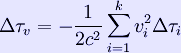
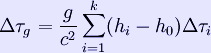
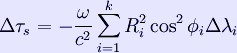 i
i