Sphere packing

In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing problems can be generalised to consider unequal spheres, n-dimensional Euclidean space (where the problem becomes circle packing in two dimensions, or hypersphere packing in higher dimensions) or to non-Euclidean spaces such as hyperbolic space.

A typical sphere packing problem is to find an arrangement in which the spheres fill as large a proportion of the space as possible. The proportion of space filled by the spheres is called the density of the arrangement. As the local density of a packing in an infinite space can vary depending on the volume over which it is measured, the problem is usually to maximise the average or asymptotic density, measured over a large enough volume.

Classification and terminology

A lattice arrangement (commonly called a regular arrangement) is one in which the centers of the spheres form a very symmetric pattern which only needs n vectors to be uniquely defined (in n-dimensional Euclidean space). Lattice arrangements are periodic. Arrangements in which the spheres do not form a lattice (often referred to as irregular) can still be periodic, but also aperiodic (properly speaking non-periodic) or random. Lattice arrangements are easier to handle than irregular ones—their high degree of symmetry makes it easier to classify them and to measure their densities.
Regular packing

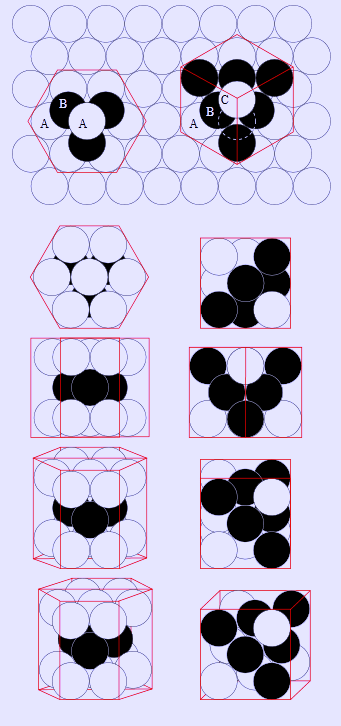
HCP lattice (left) and the FCC lattice (right) are the two most common highest density arrangements. Note that the two groups shown here are not unit cells that are capable of tessellating in 3D space. These groups do, however, readily illustrate the difference between the two lattices.
Two ways to stack three planes made of spheres

Dense packing
Main article: Close-packing of spheres

In three-dimensional Euclidean space, the densest packing of equal spheres is achieved by a family of structures called close-packed structures. One method for generating such a structure is as follows. Consider a plane with a compact arrangement of spheres on it. For any three neighbouring spheres, a fourth sphere can be placed on top in the hollow between the three bottom spheres. If we do this "everywhere" in a second plane above the first, we create a new compact layer. A third layer can be placed directly above the first one, or the spheres can be offset, vertically above another set of hollows of the first layer. There are thus three types of planes, called A, B and C.

Two simple arrangements within the close-packed family correspond to regular lattices. One is called cubic close packing (or face centred cubic) — where the layers are alternated in the ABCABC… sequence. The other is called hexagonal close packing — where the layers are alternated in the ABAB… sequence. But many layer stacking sequences are possible (ABAC, ABCBA, ABCBAC, etc.), and still generate a close-packed structure. In all of these arrangements each sphere is surrounded by 12 other spheres, and the average density is

\( \frac{\pi}{\sqrt{18}} \simeq 0.74048. \)

Gauss proved in 1831 that these packings have the highest density amongst all possible lattice packings.[1]

In 1611 Johannes Kepler had conjectured that this is the maximum possible density amongst both regular and irregular arrangements — this became known as the Kepler conjecture. In 1998 Thomas Callister Hales, following the approach suggested by László Fejes Tóth in 1953, announced the proof of the Kepler conjecture. Hales' proof is a proof by exhaustion involving checking of many individual cases using complex computer calculations. Referees have said that they are "99% certain" of the correctness of Hales' proof, so the Kepler conjecture has almost certainly been proved.
Other common lattice packings

Some other lattice packings are often found in physical systems. These include the cubic lattice with a density of \( \frac{\pi}{6} \), the hexagonal lattice with a density of \( \frac{\pi}{3\sqrt{3}} \), and the tetrahedral lattice with a density of \( \frac{\pi\sqrt{3}}{16} \).
Jammed packings with a low density

Packings where all spheres are constrained by their neighbours to stay in one location are called rigid or jammed. The locally jammed sphere packing with the lowest density has a density of only 0.0555.[2]
Irregular packing
Main article: Random close pack

If we attempt to build a densely packed collection of spheres we will be tempted to always place the next sphere in a hollow between three packed spheres. If five spheres are assembled in this way, they will be consistent with one of the regularly packed arrangements described above. However, the sixth sphere placed in this way will render the structure inconsistent with any regular arrangement. This results in the possibility of a random close packing of spheres which is stable against compression.[3]

When spheres are randomly added to a container and then compressed, they will generally form what is known as an "irregular" or "jammed" packing configuration when they can be compressed no more. This irregular packing will generally have a density of about 64%. Recent research predicts analytically that it cannot exceed a density limit of 63.4%[4] This situation is unlike the case of one or two dimensions, where compressing a collection of 1-dimensional or 2-dimensional spheres (i.e. line segments or disks) will yield a regular packing.
Hypersphere packing

The sphere packing problem is the three-dimensional version of a class of ball-packing problems in arbitrary dimensions. In two dimensions, the equivalent problem is packing circles on a plane.

In dimensions higher than three, the densest regular packings of hyperspheres are known up to 8 dimensions.[5] Very little is known about irregular hypersphere packings; it is possible that in some dimensions the densest packing may be irregular. Some support for this conjecture comes from the fact that in certain dimensions (e.g. 10) the densest known irregular packing is denser than the densest known regular packing.[6]

Dimension 24 is special due to the existence of the Leech lattice, which has the best kissing number and is the densest lattice packing. No better irregular packing is known, and at best an irregular packing could improve over the Leech lattice packing by only 2×10⁻³⁰.[7]

Another line of research in high dimensions is trying to find asymptotic bounds for the density of the densest packings. Currently the best known result is that there exists a lattice in dimension n with density bigger or equal to \( cn2^{-n} \) for some number c.[8]
Unequal sphere packing
A dense packing of spheres with a radius ratio of 0.648

Many problems in the chemical and physical sciences can be related to packing problems where more than one size of sphere is available. Here there is a choice between separating the spheres into regions of close-packed equal spheres, or combining the multiple sizes of spheres into a compound or interstitial packing. When many sizes of spheres (or a distribution) are available, the problem quickly becomes untractable, but some studies of binary hard spheres (two sizes) are available.

When the second sphere is much smaller than the first, it is possible to arrange the large spheres in a close-packed arrangement, and then arrange the small spheres within the octahedral and tetrahedral gaps. The density of this interstitial packing depends sensitively on the radius ratio, but in the limit of extreme size ratios, the smaller spheres can fill the gaps with the same density as the larger spheres filled space.[9]

When the smaller sphere has a radius greater than 0.4142 of the radius of the larger sphere, it is no longer possible to fit into even the octahedral holes of the close-packed structure. Thus, beyond this point, either the host structure must expand to accommodate the interstitials (which compromises the overall density), or rearrange into a more complex crystalline compound structure. Structures are known which exceed the close packing density for radius ratios up to 0.659786.[10][11]
Hyperbolic space

Although the concept of circles and spheres can be extended to hyperbolic space, finding the densest packing becomes much more difficult. In a hyperbolic space there is no limit to the number of spheres that can surround another sphere (for example, Ford circles can be thought of as an arrangement of identical hyperbolic circles in which each circle is surrounded by an infinite number of other circles). The concept of average density also becomes much more difficult to define accurately. The densest packings in any hyperbolic space are almost always irregular.[12]
Other spaces

Sphere packing on the corners of a hypercube (with the spheres defined by Hamming distance) corresponds to designing error-correcting codes: if the spheres have radius d, then their centers are codewords of a d-error-correcting code. Lattice packings correspond to linear codes. There are other, subtler relationships between Euclidean sphere packing and error-correcting codes. For example, the binary Golay code is closely related to the 24-dimensional Leech lattice.
See also

Apollonian sphere packing
Hermite constant
Kissing number problem
Sphere-packing bound

References

^ C.F. Gauss (1831). "Besprechung des Buchs von L.A. Seeber: Intersuchungen über die Eigenschaften der positiven ternären quadratischen Formen usw". Göttingsche Gelehrte Anzeigen.
^ Gardner, Martin (1983). Martin Gardner's new mathematical diversions from Scientific American. Chicago: University of Chicago Press. pp. 82–90. ISBN 0-226-28247-3.
^ Chaikin, Paul (June 2007). "Random thoughts". Physics Today (American Institute of Physics) 60 (6): 8. Bibcode 2007PhT....60f...8C. doi:10.1063/1.2754580. ISSN 0031-9228.
^ Song, C.; Wang, P. & Makse,H.A. (29 May 2008). "A phase diagram for jammed matter". Nature 453 (7195): 629–632. Bibcode 2008Natur.453..629S. doi:10.1038/nature06981. PMID 18509438.
^ Weisstein, Eric W., "Hypersphere Packing" from MathWorld.
^ Sloane, N. J. A. (1998). "The Sphere-Packing Problem". Documenta Mathematika 3: 387–396. arXiv:math/0207256v1. Bibcode 2002math......7256S.
^ Cohn, Henry; Kumar, Abhinav (2004). "The densest lattice in twenty-four dimensions". Electronic Research Announcements of the American Mathematical Society 10 (07): 58–67. arXiv:math.MG/0403263. doi:10.1090/S1079-6762-04-00130-1. ISSN 1079-6762. MR2075897.
^ Rogers, C. A. (1947). "Existence Theorems in the Geometry of Numbers". The Annals of Mathematics, 2nd Ser. 48 (4): 994–1002. JSTOR 1969390.
^ Hudson, D. R. (1949). "Density and Packing in an Aggregate of Mixed Spheres". Journal of Applied Physics 20 (2): 154–162. doi:10.1063/1.1698327. edit
^ Marshall, G. W.; Hudson, T. S. (2010). "Dense binary sphere packings". Contributions to Algebra and Geometry 51 (2): 337–344.
^ O’Toole, P. I.; Hudson, T. S. (2011). "New High-Density Packings of Similarly Sized Binary Spheres". The Journal of Physical Chemistry C 115 (39): 19037. doi:10.1021/jp206115p. edit
^ Bowen, L.; Radin, C. (2002). "Densest Packing of Equal Spheres in Hyperbolic Space". Discrete and Computational Geometry 29: 23–39. doi:10.1007/s00454-002-2791-7. edit

Bibliography

Aste T, Weaire D (2000). The Pursuit of Perfect Packing. London: Institute of Physics Publishing. ISBN 0-750-30648-3.
Conway JH, Sloane NJH (1998). Sphere Packings, Lattices and Groups (3rd ed.). ISBN 0-387-98585-9.
Sloane, N. J. A. (1984). "The Packing of Spheres". Scientific American 250: 116–125. Bibcode 1984SciAm.250..116G.

External links

Dana Mackenzie (May 2002) "A fine mess" (New Scientist)

A non-technical overview of packing in hyperbolic space.

Weisstein, Eric W., "Circle Packing" from MathWorld.
"Kugelpackungen (Sphere Packing)" (T.E. Dorozinski)
"3D Sphere Packing Applet" Sphere Packing java applet
"Densest Packing of spheres into a sphere" java applet

Mathematics Encyclopedia