.
Iterated function system
In mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar.
IFS fractals, as they are normally called, can be of any number of dimensions, but are commonly computed and drawn in 2D. The fractal is made up of the union of several copies of itself, each copy being transformed by a function (hence "function system"). The canonical example is the Sierpiński gasket, also called the Sierpiński triangle. The functions are normally contractive, which means they bring points closer together and make shapes smaller. Hence, the shape of an IFS fractal is made up of several possibly-overlapping smaller copies of itself, each of which is also made up of copies of itself, ad infinitum. This is the source of its self-similar fractal nature.
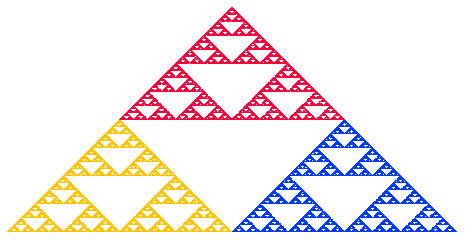
Sierpinski gasket created using IFS (colored to illustrate self-similar structure)
Definition
Formally, an iterated function system is a finite set of contraction mappings on a complete metric space.[1] Symbolically,
\( \{f_i:X\to X|i=1,2,\dots,N\},\ N\in\mathbb{N} \)
is an iterated function system if each \( f_i \) is a contraction on the complete metric space X.
Properties
Hutchinson (1981) showed that, for the metric space \( \mathbb{R}^n \), such a system of functions has a unique nonempty compact (closed and bounded) fixed set S. One way of constructing a fixed set is to start with an initial point or set S0 and iterate the actions of the fi, taking Sn+1 to be the union of the images of Sn under the fi ; then taking S to be the closure of the union of the Sn. Symbolically, the unique fixed (nonempty compact) set \( S\subseteq X \) has the property
\( S = \bigcup_{i=1}^N f_i(S). \)
The set S is thus the fixed set of the Hutchinson operator
\( H(A)=\bigcup_{i=1}^N f_i(A). \)
The existence and uniqueness of S is a consequence of the contraction mapping principle, as is the fact that
\( \lim_{n\to\infty}H^{\circ n}(A)=S \)
for any nonempty compact set A in X. (For contractive IFS this convergence takes place even for any nonempty closed bounded set A). Random elements arbitrarily close to S may be obtained by the "chaos game," described below.
Recently it was shown that the IFSs of noncontractive type (i.e. composed of maps that are not contractions with respect to any topologically equivalent metric in X) can yield attractors.
These arise naturally in projective spaces, though classical irrational rotation on the circle can be adapted too.[2]
The collection of functions f_i generates a monoid under composition. If there are only two such functions, the monoid can be visualized as a binary tree, where, at each node of the tree, one may compose with the one or the other function (i.e. take the left or the right branch). In general, if there are k functions, then one may visualize the monoid as a full k-ary tree, also known as a Cayley tree.
Constructions

Construction of an IFS by the chaos game (animated) (*)
Sometimes each function f_i is required to be a linear, or more generally an affine, transformation, and hence represented by a matrix. However, IFSs may also be built from non-linear functions, including projective transformations and Möbius transformations. The Fractal flame is an example of an IFS with nonlinear functions.
The most common algorithm to compute IFS fractals is called the "chaos game". It consists of picking a random point in the plane, then iteratively applying one of the functions chosen at random from the function system to transform the point to get a next point. An alternative algorithm is to generate each possible sequence of functions up to a given maximum length, and then to plot the results of applying each of these sequences of functions to an initial point or shape.
Each of these algorithms provides a global construction which generates points distributed across the whole fractal. If a small area of the fractal is being drawn, many of these points will fall outside of the screen boundaries. This makes zooming into an IFS construction drawn in this manner impractical.
Although the theory of IFS requires each function to be contractive, in practice software that implements IFS only require that the whole system be contractive on average.[3]
Examples

IFS being made with two functions. (*)
Barnsley's fern, an early IFS
The diagram shows the construction on an IFS from two affine functions. The functions are represented by their effect on the bi-unit square (the function transforms the outlined square into the shaded square). The combination of the two functions forms the Hutchinson operator. Three iterations of the operator are shown, and then the final image is of the fixed point, the final fractal.
Early examples of fractals which may be generated by an IFS include the Cantor set, first described in 1884; and de Rham curves, a type of self-similar curve described by Georges de Rham in 1957.
History
IFSs were conceived in their present form by John E. Hutchinson in 1981[4] and popularized by Michael
Barnsley's book Fractals Everywhere.
"IFSs provide models for certain plants, leaves, and ferns, by virtue of the self-similarity which often occurs in branching structures in nature."
—Michael Barnsley et al.[5]
See also
Menger sponge, a 3-Dimensional IFS.
Collage theorem
L-system
Fractal compression
Fractal flame
Complex base systems
Infinite compositions of analytic functions
Notes
Michael Barnsley, "Fractals Everywhere", Academic Press, Inc., 1988.
M. Barnsley, A. Vince, The Chaos Game on a General Iterated Function System
Draves, Scott; Erik Reckase (July 2007). "The Fractal Flame Algorithm" (PDF). Retrieved 2008-07-17.
Hutchinson, John E. (1981). "Fractals and self similarity" (PDF). Indiana Univ. Math. J. 30 (5): 713–747. doi:10.1512/iumj.1981.30.30055.
Michael Barnsley, et al.,"V-variable fractals and superfractals" PDF (2.22 MB)
References
Draves, Scott; Erik Reckase (July 2007). "The Fractal Flame Algorithm" (PDF). Retrieved 2008-07-17.
Falconer, Kenneth (1990). Fractal geometry: Mathematical foundations and applications. John Wiley and Sons. pp. 113–117, 136. ISBN 0-471-92287-0.
Barnsley, Michael; Andrew Vince (2010). "The Chaos Game on a General Iterated Function System" (PDF). Ergodic Theory Dynam. Systems 31 (2011), no. 4, 1073–1079. Retrieved 2013-06-05.
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

