Cassini projection

The Cassini projection is a map projection described by César-François Cassini de Thury in 1745.[1] It is the transverse aspect of the equirectangular projection, in that the globe is first rotated so the central meridian becomes the "equator", and then the normal equirectangular projection is applied. Composing these operations:

\( x = \arcsin(\cos(\phi)\sin(\lambda))\, \)

\( y = \arctan\left(\frac{\tan(\phi)}{\cos(\lambda)}\right) \)

where \( \lambda \) is the longitude from the central meridian and \( \phi \) is the latitude. When programming these equations, the inverse tangent function used is actually the atan2 function, with the first argument \( \sin(\phi) \) and the second \( \cos(\phi)\cos(\lambda) \) .

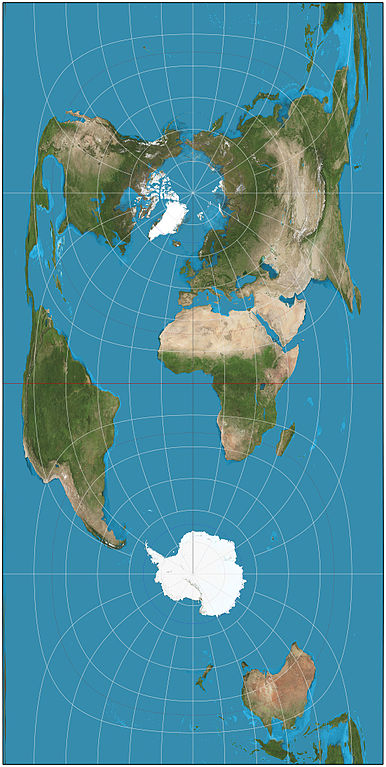
Cassini projection (*)

The use of the Cassini projection has largely been superseded by the Transverse Mercator projection, at least with central mapping agencies.
Distortions

Things along the central meridian, and at right angles to it, are not distorted. Elsewhere, the distortion is largely in a north-south direction, and varies by the square of the central meridian. As such, the greater the longitudinal extent of the area, the worse the distortion becomes.

Due to this, the Cassini projection works best on long, narrow areas, and worst on wide areas.
References

^ Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, 1993, pp. 74–76, ISBN 0-226-76747-7.

External links

Table of examples and properties of all common projections, from radicalcartography.net
Ordnance Survey GeoFacts on the Cassini Projection

Mathematics Encyclopedia