Casey's Theorem

In mathematics, Casey's theorem, also known as the generalized Ptolemy's theorem, is a theorem in Euclidean geometry named after the Irish mathematician John Casey.

\( t_{12} \cdot t_{34}+t_{14}\cdot t_{23}-t_{13}\cdot t_{24}=0 \)(*)

Formulation of the theorem

\( t_{12} \cdot t_{34}+t_{14}\cdot t_{23}-t_{13}\cdot t_{24}=0 \)

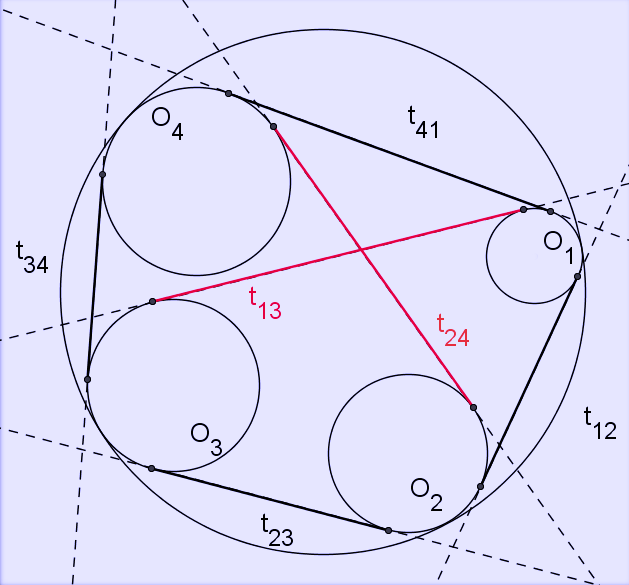
Let \( \,O \) be a circle of radius \( \,R \) . Let \( \,O_1, O_2, O_3, O_4 \) be (in that order) four non-intersecting circles that lie inside \( \,O \) and tangent to it. Denote by \( \,t_{ij} \) the length of the exterior common tangent of the circles \( \,O_i, O_j \) . Then[1]:

\( \,t_{12} \cdot t_{34}+t_{14} \cdot t_{23}=t_{13}\cdot t_{24}.\)

Note that in the degenerate case, where all four circles reduce to points, this is exactly Ptolemy's theorem.
Proof

The following proof is due[2] to Zacharias[3]. Denote the radius of circle \( \,O_i \) by \( \,R_i \) and its tangency point with the circle \( \,O \) by \( \,K_i.\) We will use the notation \( \,O, O_i \) for the centers of the circles. Note that from Pythagorean theorem,

\( \,t_{ij}^2=\overline{O_iO_j}^2-(R_i-R_j)^2.\)

We will try to express this length in terms of the points \( \,K_i,K_j.\) By the law of cosines in triangle \( \,O_iOO_j, \)

\( \overline{O_iO_j}^2=\overline{OO_i}^2+\overline{OO_j}^2-2\overline{OO_i}\cdot \overline{OO_j}\cdot \cos\angle O_iOO_j\)

Since the circles \( \,O,O_i \) tangent to each other:

\( \overline{OO_i} = R - R_i,\, \angle O_iOO_j = \angle K_iOK_j \)

Let \,C \) be a point on the circle \( \,O \). According to the law of sines in triangle \( \,K_iCK_j: \)

\( \overline{K_iK_j} = 2R\cdot \sin\angle K_iCK_j = 2R\cdot \sin\frac{\angle K_iOK_j}{2} \)

Therefore,

\( \cos\angle K_iOK_j = 1-2\sin^2\frac{\angle K_iOK_j}{2}=1-2\cdot \) \left(\frac{\overline{K_iK_j}}{2R}\right)^2 = 1 - \frac{\overline{K_iK_j}^2}{2R^2} \)

and substituting these in the formula above:

\( \overline{O_iO_j}^2=(R-R_i)^2+(R-R_j)^2-2(R-R_i)(R-R_j)\left(1-\frac{\overline{K_iK_j}^2}{2R^2}\right) \)

\( \overline{O_iO_j}^2=(R-R_i)^2+(R-R_j)^2-2(R-R_i)(R-R_j)+(R-R_i)(R-R_j)\cdot \frac{\overline{K_iK_j}^2}{R^2} \)

\( \overline{O_iO_j}^2=((R-R_i)-(R-R_j))^2+(R-R_i)(R-R_j)\cdot \frac{\overline{K_iK_j}^2}{R^2} \)

And finally, the length we seek is

\( t_{ij}=\sqrt{\overline{O_iO_j}^2-(R_i-R_j)^2}=\frac{\sqrt{R-R_i}\cdot \sqrt{R-R_j}\cdot \overline{K_iK_j}}{R} \)

We can now evaluate the left hand side, with the help of the original Ptolemy's theorem applied to the inscribed quadrilateral \( \,K_1K_2K_3K_4: \)

\( t_{12}t_{34}+t_{14}t_{23}=\frac{1}{R^2}\cdot \sqrt{R-R_1}\sqrt{R-R_2}\sqrt{R-R_3}\sqrt{R-R_4}\left(\overline{K_1K_2}\cdot \overline{K_3K_4}+\overline{K_1K_4}\cdot \overline{K_2K_3}\right) \)

\( =\frac{1}{R^2}\cdot \sqrt{R-R_1}\sqrt{R-R_2}\sqrt{R-R_3}\sqrt{R-R_4}\left(\overline{K_1K_3}\cdot \overline{K_2K_4}\right)=t_{13}t_{24} \)

Q.E.D.
Further generalizations

It can be seen that the four circles need not lie inside the big circle. In fact, they may be tangent to it from the outside as well. In that case, the following change should be made[4]:

If \( \,O_i, O_j \) are both tangent from the same side of \( \,O \) (both in or both out), \( \,t_{ij} \) is the length of the exterior common tangent.

If \( \,O_i, O_j \) are tangent from different sides of \( \,O (one in and one out), \( \,t_{ij} \) is the length of the interior common tangent.

It is also worth noting that the converse of this statement is also true[4]. That is, if equality holds, the circles are tangent.
Applications

Casey's theorem and its converse can be used to prove a variety of statements in Euclidean geometry.

For example, the shortest known proof[1] of Feuerbach's theorem uses the converse theorem.
References

^ a b Casey, J. (1866), Math. Proc. R. Ir. Acad. 9: 396.
^ Bottema, O. (1944), Hoofdstukken uit de Elementaire Meetkunde, (translation by Reinie Erné as Topics in Elementary Geometry, Springer 2008, of the second extended edition published by Epsilon-Uitgaven 1987).
^ Zacharias, M. (1942), Jahresbericht der Deutschen Mathematiker-Vereinigung 52.
^ a b Johnson, Roger A. (1929), Modern Geometry, Houghton Mifflin, Boston (republished facsimile by Dover 1960, 2007 as Advanced Euclidean Geometry).

External links

Weisstein, Eric W., "Casey's theorem" from MathWorld.
Shailesh Shirali: On a generalized Ptolemy Theorem