.
Airy function
In the physical sciences, the Airy function Ai(x) is a special function named after the British astronomer George Biddell Airy (1801–92). The function Ai(x) and the related function Bi(x), which is also called the Airy function, but sometimes referred to as the Bairy function, are solutions to the differential equation
\( \frac{d^2y}{dx^2} - xy = 0 , \,\! \)
known as the Airy equation or the Stokes equation. This is the simplest second-order linear differential equation with a turning point (a point where the character of the solutions changes from oscillatory to exponential).
The Airy function is the solution to Schrödinger's equation for a particle confined within a triangular potential well and for a particle in a one-dimensional constant force field. For the same reason, it also serves to provide uniform semiclassical approximations near a turning point in the WKB method, when the potential may be locally approximated by a linear function of position. The triangular potential well solution is directly relevant for the understanding of many semiconductor devices.
The Airy function also underlies the form of the intensity near an optical directional caustic, such as that of the rainbow. Historically, this was the mathematical problem that led Airy to develop this special function.
Definitions
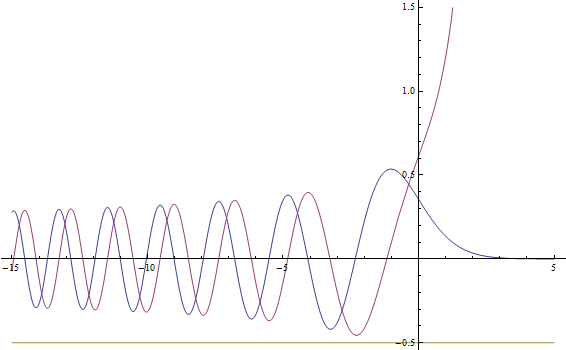
Plot of Ai(x) in red and Bi(x) in blue.
For real values of x, the Airy function is defined by the improper integral
\( \mathrm{Ai}(x) = \frac{1}{\pi} \int_0^\infty \cos\left(\tfrac13t^3 + xt\right)\, dt, \)
which converges because the positive and negative parts of the rapid oscillations tend to cancel one another out (as can be checked by integration by parts).
By differentiating under the integration sign, we find that y = Ai(x) satisfies the differential equation
\( y'' - xy = 0 . \,\! \)
This equation has two linearly independent solutions. The standard choice for the other solution is the Airy function of the second kind, denoted Bi(x). It is defined as the solution with the same amplitude of oscillation as Ai(x) as x goes to −∞ which differs in phase by π/2:
\( \mathrm{Bi}(x) = \frac{1}{\pi} \int_0^\infty \left[\exp\left(-\tfrac13t^3 + xt\right) + \sin\left(\tfrac13t^3 + xt\right)\,\right]dt. \)
Properties
The values of Ai(x) and Bi(x) and their derivatives at x = 0 are given by
\( \begin{align} \mathrm{Ai}(0) &{}= \frac{1}{3^{2/3}\Gamma(\tfrac23)}, & \quad \mathrm{Ai}'(0) &{}= -\frac{1}{3^{1/3}\Gamma(\tfrac13)}, \\ \mathrm{Bi}(0) &{}= \frac{1}{3^{1/6}\Gamma(\tfrac23)}, & \quad \mathrm{Bi}'(0) &{}= \frac{3^{1/6}}{\Gamma(\tfrac13)}. \end{align} \)
Here, Γ denotes the Gamma function. It follows that the Wronskian of Ai(x) and Bi(x) is 1/π.
When x is positive, Ai(x) is positive, convex, and decreasing exponentially to zero, while Bi(x) is positive, convex, and increasing exponentially. When x is negative, Ai(x) and Bi(x) oscillate around zero with ever-increasing frequency and ever-decreasing amplitude. This is supported by the asymptotic formulae below for the Airy functions.
The Airy functions are orthogonal[1] in the sense that
\( \int_{-\infty}^\infty \mathrm{Ai}(t+x) \mathrm{Ai}(t+y) dt = \delta(x-y). \)
Asymptotic formulae
The asymptotic behaviour of the Airy functions as x goes to +∞ is given by the following asymptotic formulae:[2]
\( \begin{align} \mathrm{Ai}(x) &{}\sim \frac{e^{-\frac{2}{3}x^{3/2}}}{2\sqrt\pi\,x^{1/4}} \\[6pt] \mathrm{Bi}(x) &{}\sim \frac{e^{\frac{2}{3}x^{3/2}}}{\sqrt\pi\,x^{1/4}}. \end{align} \)
For the limit in the negative direction we have[3]
\( \begin{align} \mathrm{Ai}(-x) &{}\sim \frac{\sin \left(\frac23x^{3/2}+\frac14\pi \right)}{\sqrt\pi\,x^{1/4}} \\[6pt] \mathrm{Bi}(-x) &{}\sim \frac{\cos \left(\frac23x^{3/2}+\frac14\pi \right)}{\sqrt\pi\,x^{1/4}}. \end{align} \)
Asymptotic expansions for these limits are also available. These are listed in (Abramowitz and Stegun, 1954) and (Olver, 1974).
Complex arguments
We can extend the definition of the Airy function to the complex plane by
\( \mathrm{Ai}(z) = \frac{1}{2\pi i} \int_{C} \exp\left(\tfrac{1}{3}t^3 - zt\right)\, dt, \)
where the integral is over a path C starting at the point at infinity with argument -(1/3)π and ending at the point at infinity with argument (1/3)π. Alternatively, we can use the differential equation y'' - xy = 0 to extend Ai(x) and Bi(x) to entire functions on the complex plane.
The asymptotic formula for Ai(x) is still valid in the complex plane if the principal value of x2/3 is taken and x is bounded away from the negative real axis. The formula for Bi(x) is valid provided x is in the sector {x∈C : |arg x| < (1/3)π−δ} for some positive δ. Finally, the formulae for Ai(−x) and Bi(−x) are valid if x is in the sector {x∈C : |arg x| < (2/3)π−δ}.
It follows from the asymptotic behaviour of the Airy functions that both Ai(x) and Bi(x) have an infinity of zeros on the negative real axis. The function Ai(x) has no other zeros in the complex plane, while the function Bi(x) also has infinitely many zeros in the sector {z∈C : (1/3)π < |arg z| < (1/2)π}.
Plots
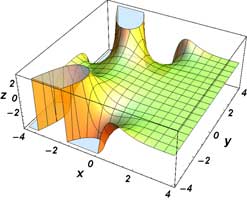
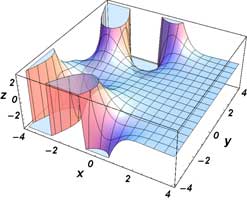
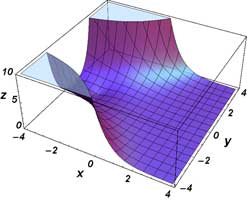
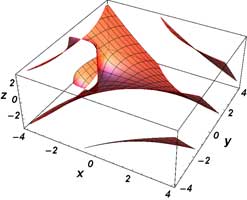
\( \Re \left[ \mathrm{Ai} ( x + iy) \right] \Im \left[ \mathrm{Ai} ( x + iy) \right] | \mathrm{Ai} ( x + iy) | \, \mathrm{arg} \left[ \mathrm{Ai} ( x + iy) \right] \, \)

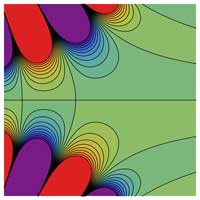

\( \Re \left[ \mathrm{Ai} ( x + iy) \right] \Im \left[ \mathrm{Ai} ( x + iy) \right] | \mathrm{Ai} ( x + iy) | \, \mathrm{arg} \left[ \mathrm{Ai} ( x + iy) \right] \, \)
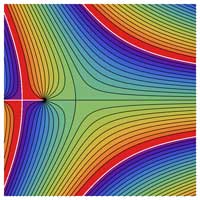
Larger Images with Contour Plots
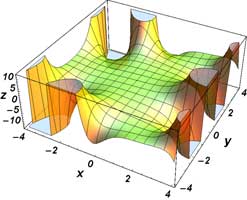

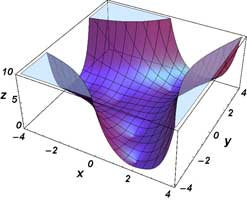
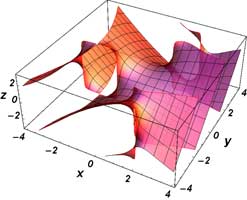
\( \Re \left[ \mathrm{Bi} ( x + iy) \right] \Im \left[ \mathrm{Bi} ( x + iy) \right] | \mathrm{Bi} ( x + iy) | \, \mathrm{arg} \left[ \mathrm{Bi} ( x + iy) \right] \, \)
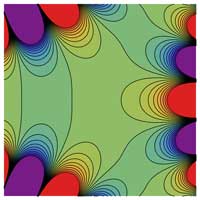
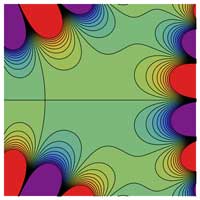
\( \Re \left[ \mathrm{Bi} ( x + iy) \right] \Im \left[ \mathrm{Bi} ( x + iy) \right] | \mathrm{Bi} ( x + iy) | \, \mathrm{arg} \left[ \mathrm{Bi} ( x + iy) \right] \, \)
Relation to other special functions
For positive arguments, the Airy functions are related to the modified Bessel functions:
\( \begin{align} \mathrm{Ai}(x) &{}= \frac1\pi \sqrt{\frac13 x} \, K_{1/3}\left(\tfrac23 x^{3/2}\right), \\ \mathrm{Bi}(x) &{}= \sqrt{\frac13 x} \left(I_{1/3}\left(\tfrac23 x^{3/2}\right) + I_{-1/3}\left(\tfrac23 x^{3/2}\right)\right). \end{align} \)
Here, I±1/3 and K1/3 are solutions of \( x^2y'' + xy' - (x^2 + 1/9)y = 0. \)
The first derivative of Airy function is
\( \mathrm{Ai'}(x) = - \frac{x} {\pi \sqrt{3}} \, K_{2/3}\left(\tfrac23 x^{3/2}\right) . \)
Functions K_{1/3} and K_{2/3} can be represented in terms of rapidly converged integrals[4] (see also modified Bessel functions )
For negative arguments, the Airy function are related to the Bessel functions:
\( \begin{align} \mathrm{Ai}(-x) &{}= \frac13 \sqrt{x} \left(J_{1/3}\left(\tfrac23 x^{3/2}\right) + J_{-1/3}\left(\tfrac23 x^{3/2}\right)\right), \\ \mathrm{Bi}(-x) &{}= \sqrt{\frac13 x} \left(J_{-1/3}\left(\tfrac23 x^{3/2}\right) - J_{1/3}\left(\tfrac23 x^{3/2}\right)\right). \end{align} \)
Here, J±1/3 are solutions of \( x^2y'' + xy' + (x^2 - 1/9)y = 0. \)
The Scorer's functions solve the equation y'' - xy = 1/\pi. They can also be expressed in terms of the Airy functions:
\( \begin{align} \mathrm{Gi}(x) &{}= \mathrm{Bi}(x) \int_x^\infty \mathrm{Ai}(t) \, dt + \mathrm{Ai}(x) \int_0^x \mathrm{Bi}(t) \, dt, \\ \mathrm{Hi}(x) &{}= \mathrm{Bi}(x) \int_{-\infty}^x \mathrm{Ai}(t) \, dt - \mathrm{Ai}(x) \int_{-\infty}^x \mathrm{Bi}(t) \, dt. \end{align} \)
Fourier transform
Using the definition of the Airy function \mathrm{Ai}(x), it is straightforward to show its Fourier transform is given by
\( \mathcal{F}(\mathrm{Ai})(k) := \int_{-\infty}^{\infty} \mathrm{Ai}(x)\ \mathrm{e}^{- 2\pi \mathrm{i} k x}\,dx = \mathrm{e}^{\frac{\mathrm{i}}{3}(2\pi k)^3}\,. \)
History
The Airy function is named after the British astronomer and physicist George Biddell Airy (1801–1892), who encountered it in his early study of optics in physics (Airy 1838). The notation Ai(x) was introduced by Harold Jeffreys. Airy had become the British Astronomer Royal in 1835, and he held that post until his retirement in 1881.
See also
The proof of Witten's conjecture used a matrix-valued generalization of the Airy function.
Notes
^ David E. Aspnes, Physical Review, 147, 554 (1966)
^ Abramowitz & Stegun (1970), Eqns 10.4.59 and 10.4.63
^ Abramowitz & Stegun (1970), Eqns 10.4.60 and 10.4.64
^ M.Kh.Khokonov. Cascade Processes of Energy Loss by Emission of Hard Photons // JETP, V.99, No.4, pp. 690-707 \ (2004).
References
Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 10", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 446, ISBN 978-0486612720, MR0167642.
Airy (1838), "On the intensity of light in the neighbourhood of a caustic", Transactions of the Cambridge Philosophical Society (University Press) 6: 379–402
Olver (1974). Asymptotics and Special Functions, Chapter 11. Academic Press, New York.
Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 6.6.3. Airy Functions", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
Vallée, Olivier; Soares, Manuel (2004), Airy functions and applications to physics, London: Imperial College Press, ISBN 978-1-86094-478-9, MR2114198
External links
Weisstein, Eric W., "Airy Functions" from MathWorld.
Wolfram function pages for Ai and Bi functions. Includes formulas, function evaluator, and plotting calculator.
Olver, F. W. J. (2010), "Airy and related functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

