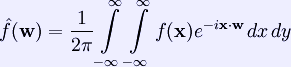|
|
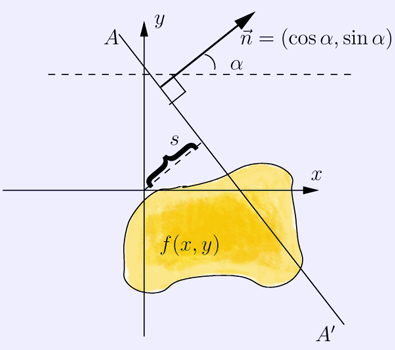
Radon transform (*) In mathematics, the Radon transform in two dimensions, named after Johann Radon, is the integral transform consisting of the integral of a function over straight lines. The inverse of the Radon transform is used to reconstruct images from medical computed tomography scans. Consider the straight line defined parametrically by (x(t),y(t)) = t(sinα, − cosα) + s(cosα,sinα) that is a distance s from the origin, and has a normal making an angle α to the x axis. We define the Radon transform of a function f on the plane (where it is assumed that the function is continuous and vanished outside a disc of some finite radius) by In n-dimensional (n>2) space the Radon transform is the integral of a function over hyperplanes. The integral of a function over the set of all lines in n-dimensional space is called the X-ray transform (or ray transform), although it is sometimes loosely referred to as a Radon transform. In the context of tomography the Radon transform data is often called a sinogram because the Radon transform of a Dirac delta function is a distribution with support on the graph of a sine wave. Consequently the Radon transform of a number of small objects appears graphically as a number of blurred sine waves with different amplitudes and phases. This transform in two dimensions and three dimensions (where a function is integrated over planes) was introduced in a 1917 paper by Johann Radon, who provided formula for the inverse transform (reconstruction problem). It was later generalised, in the context of integral geometry. The Radon transform is useful in computed axial tomography (CAT scan) and in the solution of hyperbolic partial differential equations. Fourier slice theorem Main article: Projection-slice theorem The Radon transform is closely related to the Fourier transform. For a function of one variable we define the Fourier transform
and for a function of a 2-vector and for convenience define Rα[f](s) = R[f](s,α) as we will be taking the Fourier transform in the s variable. The Fourier slice theorem then states where This result of course gives an explicit inversion formula for the Radon transform, and thus shows that it is invertible on suitably chosen spaces of functions. However it is not particularly useful for numerical inversion. Filtered back-projection An explicit and computationally efficient inversion algorithm exists for the two dimensional Radon transform called filtered back-projection. First consider the formal adjoint of R: This operator is commonly called 'back-projection' as it takes a function defined on each line in the plane and 'smears' or projects it back over the line to produce an image. Of course this adjoint is not an inverse to the Radon transform, for example the Radon transform of a small object is a function that has a thickened sine wave as its support. If this is back-projected it produces a star like image centered on the original object. We define a ramp-filter on a function h of one variable by
(the notation is not standard) then using the Fourier slice theorem and change of variables for integration we find that for f a function of two variables, and g = R[f] which means that the original image f can be recovered from the 'sinogram' data g by applying a ramp filter (in the s variable) and then backprojecting. As the filtering step can be performed efficiently (for example using digital signal processing techniques) and the back projection step is simply an accumulation of values in the pixels of the image, this results in a highly efficient, and hence widely used, algorithm. See also * Hough transform * Tomographic reconstruction References and external links * Deans, Stanley R. (1983). The Radon Transform and Some of Its Applications. New York: John Wiley & Sons. * Frank Natterer, The Mathematics of Computerized Tomography (Classics in Applied Mathematics, 32), Society for Industrial and Applied Mathematics. ISBN 0-89871-493-1 * Frank Natterer and Frank Wubbeling, Mathematical Methods in Image Reconstruction, Society for Industrial and Applied Mathematics. ISBN 0-89871-472-9 Retrieved from "http://en.wikipedia.org/"
|
|
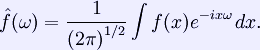 .
.