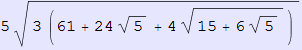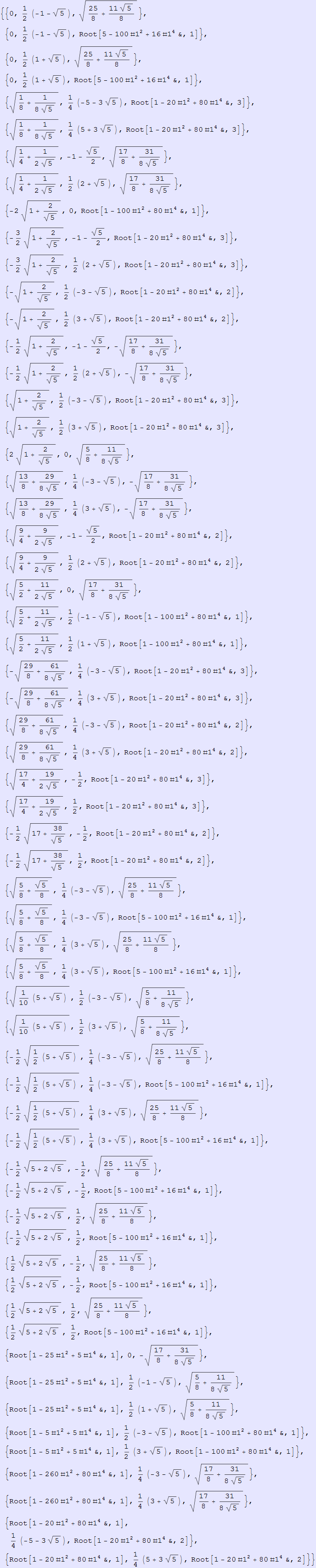In[143]:=
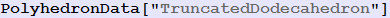
Out[143]=

In[144]:=

Out[144]=
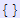
In[145]:=

Out[145]=
In[146]:=
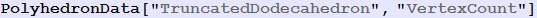
Out[146]=
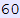
In[147]:=
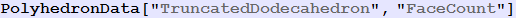
Out[147]=
In[148]:=
Out[148]=
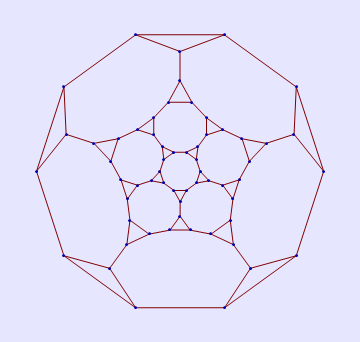
In[149]:=
Out[149]=
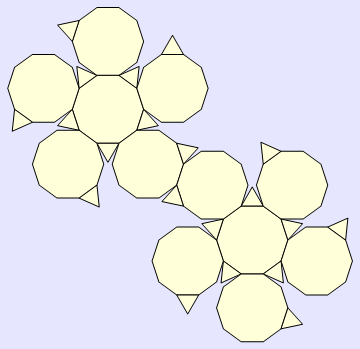
In[150]:=
Out[150]=
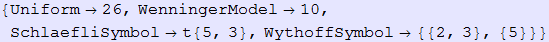
In[151]:=
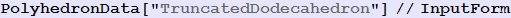
Out[151]//InputForm=
Graphics3D[GraphicsComplex[{{0, (-1 - Sqrt[5])/2, Sqrt[25/8 + (11*Sqrt[5])/8]},
{0, (-1 - Sqrt[5])/2, Root[5 - 100*#1^2 + 16*#1^4 & , 1, 0]},
{0, (1 + Sqrt[5])/2, Sqrt[25/8 + (11*Sqrt[5])/8]}, {0, (1 + Sqrt[5])/2,
Root[5 - 100*#1^2 + 16*#1^4 & , 1, 0]}, {Sqrt[1/8 + 1/(8*Sqrt[5])], (-5 - 3*Sqrt[5])/4,
Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]}, {Sqrt[1/8 + 1/(8*Sqrt[5])], (5 + 3*Sqrt[5])/4,
Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]}, {Sqrt[1/4 + 1/(2*Sqrt[5])], -1 - Sqrt[5]/2,
Sqrt[17/8 + 31/(8*Sqrt[5])]}, {Sqrt[1/4 + 1/(2*Sqrt[5])], (2 + Sqrt[5])/2,
Sqrt[17/8 + 31/(8*Sqrt[5])]}, {-2*Sqrt[1 + 2/Sqrt[5]], 0, Root[1 - 100*#1^2 + 80*#1^4 & , 1,
0]}, {(-3*Sqrt[1 + 2/Sqrt[5]])/2, -1 - Sqrt[5]/2, Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]},
{(-3*Sqrt[1 + 2/Sqrt[5]])/2, (2 + Sqrt[5])/2, Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]},
{-Sqrt[1 + 2/Sqrt[5]], (-3 - Sqrt[5])/2, Root[1 - 20*#1^2 + 80*#1^4 & , 2, 0]},
{-Sqrt[1 + 2/Sqrt[5]], (3 + Sqrt[5])/2, Root[1 - 20*#1^2 + 80*#1^4 & , 2, 0]},
{-Sqrt[1 + 2/Sqrt[5]]/2, -1 - Sqrt[5]/2, -Sqrt[17/8 + 31/(8*Sqrt[5])]},
{-Sqrt[1 + 2/Sqrt[5]]/2, (2 + Sqrt[5])/2, -Sqrt[17/8 + 31/(8*Sqrt[5])]},
{Sqrt[1 + 2/Sqrt[5]], (-3 - Sqrt[5])/2, Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]},
{Sqrt[1 + 2/Sqrt[5]], (3 + Sqrt[5])/2, Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]},
{2*Sqrt[1 + 2/Sqrt[5]], 0, Sqrt[5/8 + 11/(8*Sqrt[5])]}, {Sqrt[13/8 + 29/(8*Sqrt[5])],
(-3 - Sqrt[5])/4, -Sqrt[17/8 + 31/(8*Sqrt[5])]}, {Sqrt[13/8 + 29/(8*Sqrt[5])],
(3 + Sqrt[5])/4, -Sqrt[17/8 + 31/(8*Sqrt[5])]}, {Sqrt[9/4 + 9/(2*Sqrt[5])], -1 - Sqrt[5]/2,
Root[1 - 20*#1^2 + 80*#1^4 & , 2, 0]}, {Sqrt[9/4 + 9/(2*Sqrt[5])], (2 + Sqrt[5])/2,
Root[1 - 20*#1^2 + 80*#1^4 & , 2, 0]}, {Sqrt[5/2 + 11/(2*Sqrt[5])], 0,
Sqrt[17/8 + 31/(8*Sqrt[5])]}, {Sqrt[5/2 + 11/(2*Sqrt[5])], (-1 - Sqrt[5])/2,
Root[1 - 100*#1^2 + 80*#1^4 & , 1, 0]}, {Sqrt[5/2 + 11/(2*Sqrt[5])], (1 + Sqrt[5])/2,
Root[1 - 100*#1^2 + 80*#1^4 & , 1, 0]}, {-Sqrt[29/8 + 61/(8*Sqrt[5])], (-3 - Sqrt[5])/4,
Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]}, {-Sqrt[29/8 + 61/(8*Sqrt[5])], (3 + Sqrt[5])/4,
Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]}, {Sqrt[29/8 + 61/(8*Sqrt[5])], (-3 - Sqrt[5])/4,
Root[1 - 20*#1^2 + 80*#1^4 & , 2, 0]}, {Sqrt[29/8 + 61/(8*Sqrt[5])], (3 + Sqrt[5])/4,
Root[1 - 20*#1^2 + 80*#1^4 & , 2, 0]}, {Sqrt[17/4 + 19/(2*Sqrt[5])], -1/2,
Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]}, {Sqrt[17/4 + 19/(2*Sqrt[5])], 1/2,
Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0]}, {-Sqrt[17 + 38/Sqrt[5]]/2, -1/2,
Root[1 - 20*#1^2 + 80*#1^4 & , 2, 0]}, {-Sqrt[17 + 38/Sqrt[5]]/2, 1/2,
Root[1 - 20*#1^2 + 80*#1^4 & , 2, 0]}, {Sqrt[5/8 + Sqrt[5]/8], (-3 - Sqrt[5])/4,
Sqrt[25/8 + (11*Sqrt[5])/8]}, {Sqrt[5/8 + Sqrt[5]/8], (-3 - Sqrt[5])/4,
Root[5 - 100*#1^2 + 16*#1^4 & , 1, 0]}, {Sqrt[5/8 + Sqrt[5]/8], (3 + Sqrt[5])/4,
Sqrt[25/8 + (11*Sqrt[5])/8]}, {Sqrt[5/8 + Sqrt[5]/8], (3 + Sqrt[5])/4,
Root[5 - 100*#1^2 + 16*#1^4 & , 1, 0]}, {Sqrt[(5 + Sqrt[5])/10], (-3 - Sqrt[5])/2,
Sqrt[5/8 + 11/(8*Sqrt[5])]}, {Sqrt[(5 + Sqrt[5])/10], (3 + Sqrt[5])/2,
Sqrt[5/8 + 11/(8*Sqrt[5])]}, {-Sqrt[(5 + Sqrt[5])/2]/2, (-3 - Sqrt[5])/4,
Sqrt[25/8 + (11*Sqrt[5])/8]}, {-Sqrt[(5 + Sqrt[5])/2]/2, (-3 - Sqrt[5])/4,
Root[5 - 100*#1^2 + 16*#1^4 & , 1, 0]}, {-Sqrt[(5 + Sqrt[5])/2]/2, (3 + Sqrt[5])/4,
Sqrt[25/8 + (11*Sqrt[5])/8]}, {-Sqrt[(5 + Sqrt[5])/2]/2, (3 + Sqrt[5])/4,
Root[5 - 100*#1^2 + 16*#1^4 & , 1, 0]}, {-Sqrt[5 + 2*Sqrt[5]]/2, -1/2,
Sqrt[25/8 + (11*Sqrt[5])/8]}, {-Sqrt[5 + 2*Sqrt[5]]/2, -1/2,
Root[5 - 100*#1^2 + 16*#1^4 & , 1, 0]}, {-Sqrt[5 + 2*Sqrt[5]]/2, 1/2,
Sqrt[25/8 + (11*Sqrt[5])/8]}, {-Sqrt[5 + 2*Sqrt[5]]/2, 1/2,
Root[5 - 100*#1^2 + 16*#1^4 & , 1, 0]}, {Sqrt[5 + 2*Sqrt[5]]/2, -1/2,
Sqrt[25/8 + (11*Sqrt[5])/8]}, {Sqrt[5 + 2*Sqrt[5]]/2, -1/2,
Root[5 - 100*#1^2 + 16*#1^4 & , 1, 0]}, {Sqrt[5 + 2*Sqrt[5]]/2, 1/2,
Sqrt[25/8 + (11*Sqrt[5])/8]}, {Sqrt[5 + 2*Sqrt[5]]/2, 1/2, Root[5 - 100*#1^2 + 16*#1^4 & , 1,
0]}, {Root[1 - 25*#1^2 + 5*#1^4 & , 1, 0], 0, -Sqrt[17/8 + 31/(8*Sqrt[5])]},
{Root[1 - 25*#1^2 + 5*#1^4 & , 1, 0], (-1 - Sqrt[5])/2, Sqrt[5/8 + 11/(8*Sqrt[5])]},
{Root[1 - 25*#1^2 + 5*#1^4 & , 1, 0], (1 + Sqrt[5])/2, Sqrt[5/8 + 11/(8*Sqrt[5])]},
{Root[1 - 5*#1^2 + 5*#1^4 & , 1, 0], (-3 - Sqrt[5])/2, Root[1 - 100*#1^2 + 80*#1^4 & , 1, 0]},
{Root[1 - 5*#1^2 + 5*#1^4 & , 1, 0], (3 + Sqrt[5])/2, Root[1 - 100*#1^2 + 80*#1^4 & , 1, 0]},
{Root[1 - 260*#1^2 + 80*#1^4 & , 1, 0], (-3 - Sqrt[5])/4, Sqrt[17/8 + 31/(8*Sqrt[5])]},
{Root[1 - 260*#1^2 + 80*#1^4 & , 1, 0], (3 + Sqrt[5])/4, Sqrt[17/8 + 31/(8*Sqrt[5])]},
{Root[1 - 20*#1^2 + 80*#1^4 & , 1, 0], (-5 - 3*Sqrt[5])/4, Root[1 - 20*#1^2 + 80*#1^4 & , 2,
0]}, {Root[1 - 20*#1^2 + 80*#1^4 & , 1, 0], (5 + 3*Sqrt[5])/4,
Root[1 - 20*#1^2 + 80*#1^4 & , 2, 0]}}, Polygon[{{3, 42, 46, 44, 40, 1, 34, 48, 50, 36},
{47, 43, 4, 37, 51, 49, 35, 2, 41, 45}, {2, 35, 19, 24, 21, 16, 5, 59, 55, 14},
{49, 51, 20, 25, 29, 31, 30, 28, 24, 19}, {37, 4, 15, 56, 60, 6, 17, 22, 25, 20},
{43, 47, 52, 9, 33, 27, 11, 13, 56, 15}, {45, 41, 14, 55, 12, 10, 26, 32, 9, 52},
{6, 60, 13, 11, 54, 58, 42, 3, 8, 39}, {27, 33, 32, 26, 53, 57, 44, 46, 58, 54},
{10, 12, 59, 5, 38, 7, 1, 40, 57, 53}, {16, 21, 28, 30, 18, 23, 48, 34, 7, 38},
{31, 29, 22, 17, 39, 8, 36, 50, 23, 18}, {9, 32, 33}, {18, 30, 31}, {47, 45, 52},
{50, 48, 23}, {10, 53, 26}, {27, 54, 11}, {21, 24, 28}, {29, 25, 22}, {40, 44, 57},
{58, 46, 42}, {35, 49, 19}, {20, 51, 37}, {12, 55, 59}, {60, 56, 13}, {41, 2, 14},
{15, 4, 43}, {34, 1, 7}, {8, 3, 36}, {38, 5, 16}, {17, 6, 39}}]]]
In[152]:=
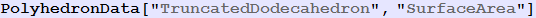
Out[152]=
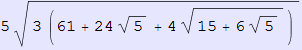
In[153]:=
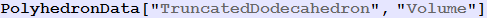
Out[153]=
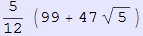
In[154]:=
Out[154]=
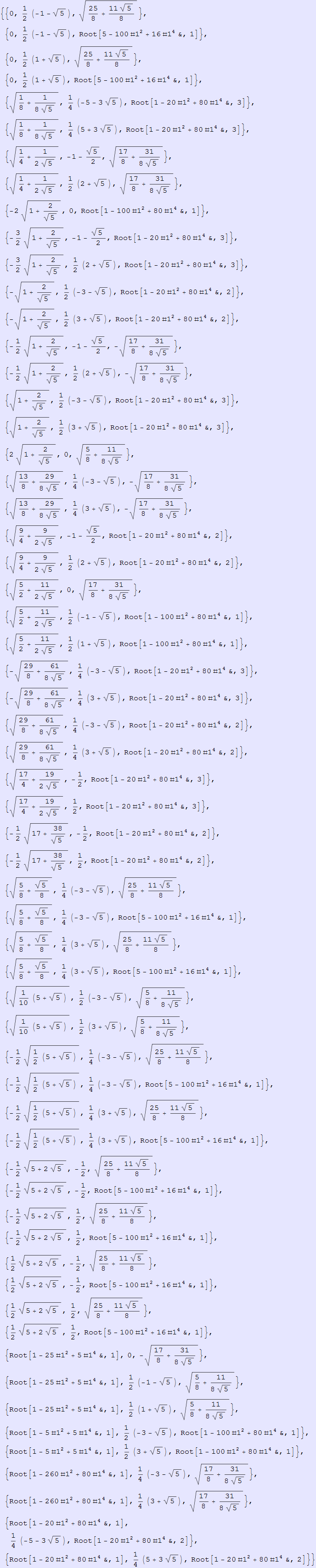
In[155]:=
Out[155]=
Archimedean Solid
Geometry