- Eric W. Weisstein, Tetrahedron at MathWorld.
- The Uniform Polyhedra
- Tetrahedron: Interactive Polyhedron Model
- K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- Paper Models of Polyhedra Many links
- An Amazing, Space Filling, Non-regular Tetrahedron that also includes a description of a "rotating ring of tetrahedra", also known as a kaleidocycle.
- Tetrahedron Core Network Application of a tetrahedral structure to create resilient partial-mesh data network
In[86]:=
Out[86]=
In[87]:=
Out[87]=
In[88]:=
Out[88]=
In[89]:=
Out[89]=
In[90]:=
Out[90]=
In[91]:=
Out[91]=
In[92]:=
Out[92]=
In[93]:=
Out[93]=
In[94]:=
Out[94]//InputForm= Graphics3D[GraphicsComplex[{{0, 0, Sqrt[2/3] - 1/(2*Sqrt[6])}, {-1/(2*Sqrt[3]), -1/2, -1/(2*Sqrt[6])}, In[95]:=
Out[95]=
In[96]:=
Out[96]=
In[97]:=
Out[97]=
A tetrahedron (plural: tetrahedra) is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral," and is one of the Platonic solids. The tetrahedron is one kind of pyramid, the second most common type; a pyramid has a flat base, and triangular faces above it, but the base can be of any polygonal shape, not just square or triangular. Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. Formulas for regular tetrahedron
Note that with respect to the base plane the slope of a face Volume of any tetrahedron The volume of any tetrahedron is given by the pyramid volume formula:
where A is the area of the base and h the height from the base to the apex. This applies for each of the four choices of the base, so the distances from the apexes to the opposite faces are inversely proportional to the areas of these faces. For a tetrahedron with vertices a = (a1, a2, a3), b = (b1, b2, b3), c = (c1, c2, c3), and d = (d1, d2, d3), the volume is (1/6)·|det(a−b, b−c, c−d)|, or any other combination of pairs of vertices that form a simply connected graph. This can be rewritten using a dot product and a cross product, yielding
If the origin of the coordinate system is chosen to coincide with vertex d, then d = 0, so
where a, b, and c represent three edges that meet at one vertex, and If we are given only the distances between the vertices of any tetrahedron, then we can compute its volume using the formula:
If the determinant's value is negative this means we can not construct a tetrahedron with the given distances between the vertexes. Moreover, for a tetrahedron ABCT the volume is given by[citation needed]
where a is angle ATB, b is angle BTC, and c is angle CTA. Distance between the edges Any two opposite edges of a tetrahedron lie on two skew lines. If the closest pair of points between these two lines are points in the edges, they define the distance between the edges; otherwise, the distance between the edges equals that between one of the endpoints and the opposite edge. Geometric relations A tetrahedron is a 3-simplex. Unlike in the case of other Platonic solids, all vertices of a regular tetrahedron are equidistant from each other (they are in the only possible arrangement of four equidistant points). A tetrahedron is a triangular pyramid, and the regular tetrahedron is self-dual. A regular tetrahedron can be embedded inside a cube in two ways such that each vertex is a vertex of the cube, and each edge is a diagonal of one of the cube's faces. For one such embedding, the Cartesian coordinates of the vertices are (+1, +1, +1); (−1, −1, +1); (−1, +1, −1); (+1, −1, −1). For the other tetrahedron (which is dual to the first), reverse all the signs. The volume of this tetrahedron is 1/3 the volume of the cube. Combining both tetrahedra gives a regular polyhedral compound called the stella octangula, whose interior is an octahedron. Correspondingly, a regular octahedron is the result of cutting off, from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e., rectifying the tetrahedron). The above embedding divides the cube into five tetrahedra, one of which is regular. In fact, 5 is the minimum number of tetrahedra required to compose a cube. Inscribing tetrahedra inside the regular compound of five cubes gives two more regular compounds, containing five and ten tetrahedra. Regular tetrahedra cannot tessellate space by themselves, although it seems likely enough that Aristotle reported it was possible. However, two regular tetrahedra can be combined with an octahedron, giving a rhombohedron which can tile space. However, there is at least one irregular tetrahedron of which copies can tile space. If one relaxes the requirement that the tetrahedra be all the same shape, one can tile space using only tetrahedra in various ways. For example, one can divide an octahedron into four identical tetrahedra and combine them again with two regular ones. (As a side-note: these two kinds of tetrahedron have the same volume.) The tetrahedron is unique among the uniform polyhedra in possessing no parallel faces. Related polyhedra Intersecting tetrahedra An interesting polyhedron can be constructed from five intersecting tetrahedra. This compound of five tetrahedra has been known for hundreds of years. It comes up regularly in the world of origami. Joining the twenty vertices would form a regular dodecahedron. There are both left-handed and right-handed forms which are mirror images of each other. The isometries of the regular tetrahedron The vertices of a cube can be grouped into two groups of four, each forming a regular tetrahedron (see above, and also animation, showing one of the two tetrahedra in the cube). The symmetries of a regular tetrahedron correspond to half of those of a cube: those which map the tetrahedrons to themselves, and not to each other. The tetrahedron is the only Platonic solid that is not mapped to itself by point inversion. The regular tetrahedron has 24 isometries, forming the symmetry group Td, isomorphic to S4. They can be categorized as follows: * T, isomorphic to alternating group A4 (the identity and 11 proper rotations) with the following conjugacy classes (in parentheses are given the permutations of the vertices, or correspondingly, the faces, and the unit quaternion representation): o identity (identity; 1) o rotation about an axis through a vertex, perpendicular to the opposite plane, by an angle of ±120°: 4 axes, 2 per axis, together 8 ((1 2 3), etc.; (1±i±j±k)/2) o rotation by an angle of 180° such that an edge maps to the opposite edge: 3 ((1 2)(3 4), etc.; i,j,k) * reflections in a plane perpendicular to an edge: 6 * reflections in a plane combined with 90° rotation about an axis perpendicular to the plane: 3 axes, 2 per axis, together 6; equivalently, they are 90° rotations combined with inversion (x is mapped to −x): the rotations correspond to those of the cube about face-to-face axes The isometries of irregular tetrahedra The isometries of an irregular tetrahedron depend on the geometry of the tetrahedron, with 7 cases possible. In each case a 3-dimensional point group is formed.
The proper rotations and reflections in the symmetry group of the regular tetrahedron (*)
* An equilateral triangle base and isosceles (and non-equilateral) triangle sides gives 6 isometries, corresponding to the 6 isometries of the base. As permutations of the vertices, these 6 isometries are the identity 1, (123), (132), (12), (13) and (23), forming the symmetry group C3v, isomorphic to S3. * Four congruent isosceles (non-equilateral) triangles gives 8 isometries. If edges (1,2) and (3,4) are of different length to the other 4 then the 8 isometries are the identity 1, reflections (12) and (34), and 180° rotations (12)(34), (13)(24), (14)(23) and improper 90° rotations (1234) and (1432) forming the symmetry group D2d. * Four congruent scalene triangles gives 4 isometries. The isometries are 1 and the 180° rotations (12)(34), (13)(24), (14)(23). This is the Klein four-group V4 ≅ Z22, present as the point group D2. * Two pairs of isomorphic isosceles (non-equilateral) triangles. This gives two opposite edges (1,2) and (3,4) that are perpendicular but different lengths, and then the 4 isometries are 1, reflections (12) and (34) and the 180° rotation (12)(34). The symmetry group is C2v, isomorphic to V4. * Two pairs of isomorphic scalene triangles. This has two pairs of equal edges (1,3), (2,4) and (1,4), (2,3) but otherwise no edges equal. The only two isometries are 1 and the rotation (12)(34), giving the group C2 isomorphic to Z2. * Two unequal isosceles triangles with a common base. This has two pairs of equal edges (1,3), (1,4) and (2,3), (2,4) and otherwise no edges equal. The only two isometries are 1 and the reflection (34), giving the group Cs isomorphic to Z2. * No edges equal, so that the only isometry is the identity, and the symmetry group is the trivial group. A law of sines for tetrahedra and the space of all shapes of tetrahedra
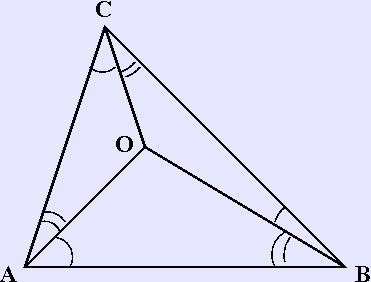
A corollary of the usual law of sines is that in a tetrahedron with vertices O, A, B, C, we have
One may view the two sides of this identity as corresponding to clockwise and counterclockwise orientations of the surface. Putting any of the four vertices in the role of O yields four such identities, but in a sense at most three of them are independent: If the "clockwise" sides of three of them are multiplied and the product is inferred to be equal to the product of the "counterclockwise" sides of the same three identities, and then common factors are cancelled from both sides, the result is the fourth identity. One reason to be interested in this "independence" relation is this: It is widely known that three angles are the angles of some triangle if and only if their sum is a half-circle. What condition on 12 angles is neceesary and sufficient for them to be the 12 angles of some tetrahedron? Clearly the sum of the angles of any side of the tetrahedron must be a half-circle. Since there are four such triangles, there are four such constraints on sums of angles, and the number of degrees of freedom is thereby reduced from 12 to 8. The four relations given by this sine law further reduce the number of degrees of freedom, not from 8 down to 4, but only from 8 down to 5, since the fourth constraint is not independent of the first three. Thus the space of all shapes of tetrahedra is 5-dimensional. Computational uses Complex shapes are often broken down into a mesh of irregular tetrahedra in preparation for finite element analysis and computational fluid dynamics studies. Applications and uses Chemistry * The tetrahedron shape is seen in nature in covalent bonds of molecules. For instance in a methane molecule (CH4) the four hydrogen atoms lie in each corner of a tetrahedron with the carbon atom in the centre. For this reason, one of the leading journals in organic chemistry is called Tetrahedron. Ammonium is another example. * Angle from the center to any two vertices is Electronics * If each edge of a tetrahedron were to be replaced by a one ohm resistor, the resistance between any two vertices would be 1/2 ohm.[1] Symbolism * The tetrahedron represents the classical element fire. Games * Especially in roleplaying, this solid is known as a d4, one of the more common polyhedral dice. * Tetrahedrons constructed of 1 1/4" PVC pipe, which were known as 'tetras', were used as the main scoring object on the 2005 FIRST Robotics Competition game Triple Play. The object of the game was to stack these 'tetras' onto larger tetrahedron goals which here placed in a 3×3 matrix. * Some Rubik's Cube-like puzzles are tetrahedral, such as the Pyraminx and Pyramorphix. Fiction * In the Xeelee Sequence of science fiction books by author Stephen Baxter, a blue-green tetrahedron is the symbol of free humanity. * The Triforces of the Legend of Zelda cartoon series are green and red tetrahedrons. The triforce's representation in the actual game series (starting in A Link to the Past) is that of an unfolded tetrahedron. * The story arc of the fan series "Star Trek: Hidden Frontier" evolves around gigantic ancient artifacts, which later become a center part of the series. The artifacts are referred to as Tetrahedrons and have the shape of such a geometrical body. In the series, the Tetrahedrons possess the ability to produce a great deal of energy and are of unknown material and origin, however, they appear to be several million years old and it is outlined that these devices have been built by an ancient civilization. See also * caltrop References 1. ^ Klein, Douglas J. (2002). "Resistance-Distance Sum Rules" (PDF). Croatica Chemica Acta 75 (2): 633–649. Retrieved on 2006-09-15. Links Retrieved from "http://en.wikipedia.org/" |
|
|||||||||||||||||||||||||||||||||||||||||

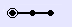



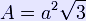
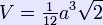
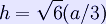
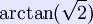
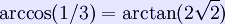
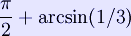
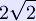 is twice that of an edge
is twice that of an edge 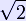 , corresponding to the fact that the horizontal distance covered from the base to the apex along an edge is twice that along the median of a face. In other words, if C is the centroid of the base, the distance from C to a vertex of the base is twice that from C to the midpoint of an edge of the base. This follows from the fact that the medians of a triangle intersect at its centroid, and this point divides each of them in two segments, one of which is twice as long as the other (see proof).
, corresponding to the fact that the horizontal distance covered from the base to the apex along an edge is twice that along the median of a face. In other words, if C is the centroid of the base, the distance from C to a vertex of the base is twice that from C to the midpoint of an edge of the base. This follows from the fact that the medians of a triangle intersect at its centroid, and this point divides each of them in two segments, one of which is twice as long as the other (see proof).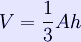
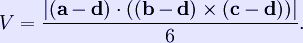 .
.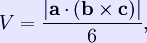 ,
,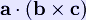 is a scalar triple product. Comparing this formula with that used to compute the volume of a parallelepiped, we conclude that the volume of a tetrahedron is equal to 1/6 of the volume of any parallelepiped which shares with it three converging edges.
is a scalar triple product. Comparing this formula with that used to compute the volume of a parallelepiped, we conclude that the volume of a tetrahedron is equal to 1/6 of the volume of any parallelepiped which shares with it three converging edges.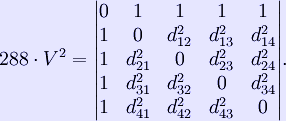
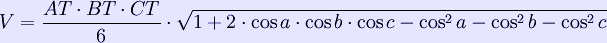

 , or approximately 109.47°.[1]
, or approximately 109.47°.[1]