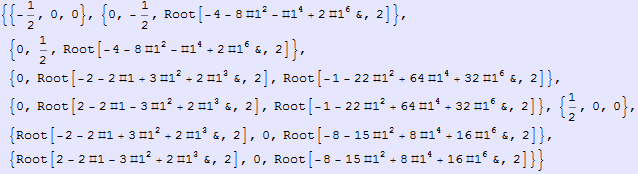In[952]:=

Out[952]=

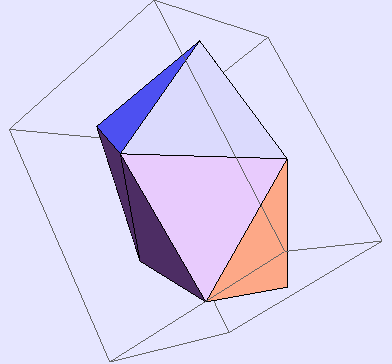
In[953]:=

Out[953]=

In[954]:=

Out[954]=

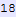
In[955]:=

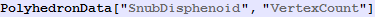
Out[955]=

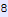
In[956]:=

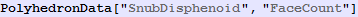
Out[956]=

In[957]:=

Out[957]=

In[958]:=

Out[958]=

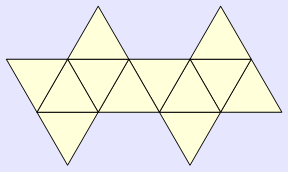
In[959]:=

Out[959]=

In[960]:=

Out[960]//InputForm=

Graphics3D[GraphicsComplex[{{-1/2, 0, -Root[-1 - 8*#1^2 - 4*#1^4 + 32*#1^6 & , 2, 0]},
   {0, -1/2, Root[-4 - 8*#1^2 - #1^4 + 2*#1^6 & , 2, 0] - Root[-1 - 8*#1^2 - 4*#1^4 + 32*#1^6 & , 2, 0]},
   {0, 1/2, Root[-4 - 8*#1^2 - #1^4 + 2*#1^6 & , 2, 0] - Root[-1 - 8*#1^2 - 4*#1^4 + 32*#1^6 & , 2, 0]},
   {0, Root[-2 - 2*#1 + 3*#1^2 + 2*#1^3 & , 2, 0], -Root[-1 - 8*#1^2 - 4*#1^4 + 32*#1^6 & , 2, 0] +
     Root[-1 - 22*#1^2 + 64*#1^4 + 32*#1^6 & , 2, 0]}, {0, Root[2 - 2*#1 - 3*#1^2 + 2*#1^3 & , 2, 0],
    -Root[-1 - 8*#1^2 - 4*#1^4 + 32*#1^6 & , 2, 0] + Root[-1 - 22*#1^2 + 64*#1^4 + 32*#1^6 & , 2, 0]},
   {1/2, 0, -Root[-1 - 8*#1^2 - 4*#1^4 + 32*#1^6 & , 2, 0]}, {Root[-2 - 2*#1 + 3*#1^2 + 2*#1^3 & , 2, 0], 0,
    Root[-8 - 15*#1^2 + 8*#1^4 + 16*#1^6 & , 2, 0] - Root[-1 - 8*#1^2 - 4*#1^4 + 32*#1^6 & , 2, 0]},
   {Root[2 - 2*#1 - 3*#1^2 + 2*#1^3 & , 2, 0], 0, Root[-8 - 15*#1^2 + 8*#1^4 + 16*#1^6 & , 2, 0] -
     Root[-1 - 8*#1^2 - 4*#1^4 + 32*#1^6 & , 2, 0]}}, Polygon[{{2, 3, 7}, {3, 2, 8}, {4, 2, 7}, {2, 4, 8}, {6, 8, 4}, {4, 1, 6}, {7, 1, 4},
    {3, 5, 7}, {8, 5, 3}, {5, 8, 6}, {5, 6, 1}, {5, 1, 7}}]]]

In[961]:=

Out[961]=

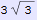
In[962]:=

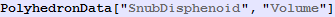
Out[962]=

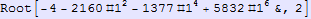
In[963]:=

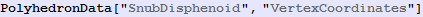
Out[963]=

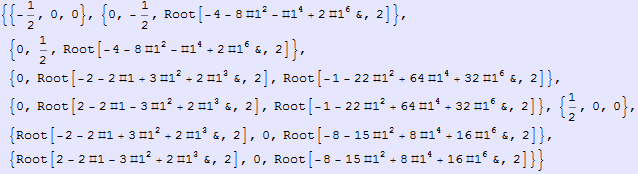
Johnson Polyhedra

Geometry