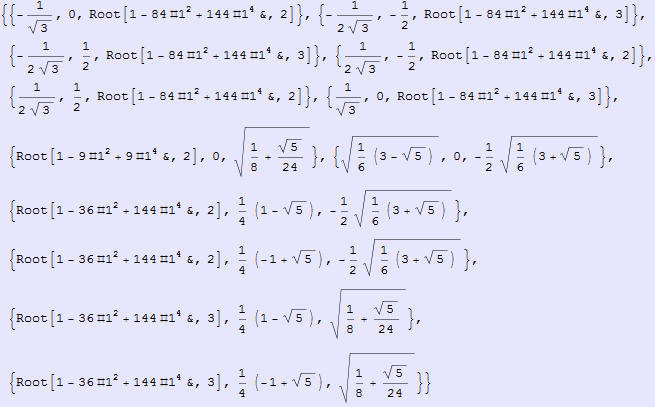In[148]:=

Out[148]=

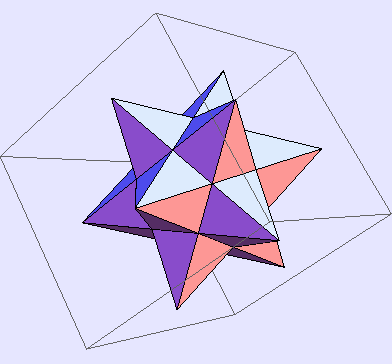
In[149]:=

Out[149]=

In[150]:=

Out[150]=

In[151]:=

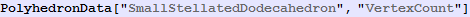
Out[151]=

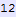
In[152]:=

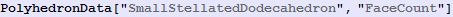
Out[152]=

In[153]:=

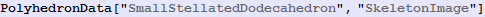
Out[153]=

In[154]:=

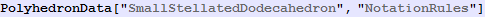
Out[154]=

In[155]:=

Out[155]//InputForm=

Graphics3D[GraphicsComplex[{{-(1/Sqrt[3]), 0, Root[1 - 84*#1^2 + 144*#1^4 & , 2, 0]},
   {-1/(2*Sqrt[3]), -1/2, Root[1 - 84*#1^2 + 144*#1^4 & , 3, 0]}, {-1/(2*Sqrt[3]), 1/2, Root[1 - 84*#1^2 + 144*#1^4 & , 3, 0]},
   {1/(2*Sqrt[3]), -1/2, Root[1 - 84*#1^2 + 144*#1^4 & , 2, 0]}, {1/(2*Sqrt[3]), 1/2, Root[1 - 84*#1^2 + 144*#1^4 & , 2, 0]},
   {1/Sqrt[3], 0, Root[1 - 84*#1^2 + 144*#1^4 & , 3, 0]}, {Root[1 - 9*#1^2 + 9*#1^4 & , 2, 0], 0, Sqrt[1/8 + Sqrt[5]/24]},
   {Sqrt[(3 - Sqrt[5])/6], 0, -Sqrt[(3 + Sqrt[5])/6]/2}, {Root[1 - 36*#1^2 + 144*#1^4 & , 2, 0], (1 - Sqrt[5])/4, -Sqrt[(3 + Sqrt[5])/6]/2},
   {Root[1 - 36*#1^2 + 144*#1^4 & , 2, 0], (-1 + Sqrt[5])/4, -Sqrt[(3 + Sqrt[5])/6]/2}, {Root[1 - 36*#1^2 + 144*#1^4 & , 3, 0], (1 - Sqrt[5])/4,
    Sqrt[1/8 + Sqrt[5]/24]}, {Root[1 - 36*#1^2 + 144*#1^4 & , 3, 0], (-1 + Sqrt[5])/4, Sqrt[1/8 + Sqrt[5]/24]}},
  Polygon[{{2, 12, 1, 11, 3}, {10, 4, 1, 8, 2}, {3, 8, 1, 5, 9}, {9, 11, 1, 4, 7}, {7, 5, 1, 12, 10}, {7, 10, 2, 3, 9}, {4, 12, 2, 6, 7},
    {9, 6, 2, 8, 11}, {7, 6, 3, 11, 5}, {12, 8, 3, 6, 10}, {9, 5, 4, 10, 6}, {8, 12, 4, 5, 11}}]]]

In[156]:=

Out[156]=

In[157]:=

Out[157]=

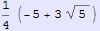
In[158]:=

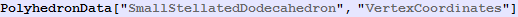
Out[158]=

Kepler-Poinsot Polyhedra