.
Ptolemy's theorem
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral (a quadrilateral whose vertices lie on a common circle). The theorem is named after the Greek astronomer and mathematician Ptolemy (Claudius Ptolemaeus).[1] Ptolemy used the theorem as an aid to creating his table of chords, a trigonometric table that he applied to astronomy.
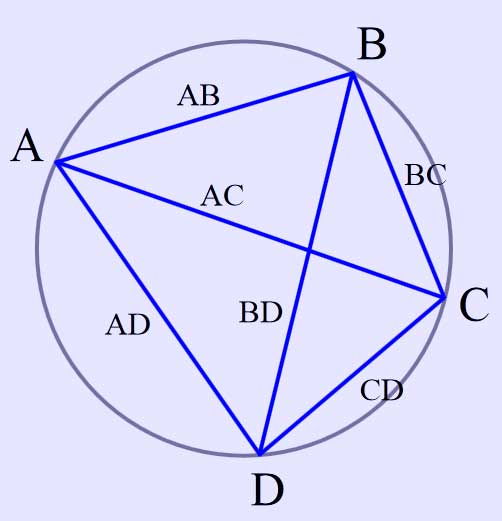
If the quadrilateral is given with its four vertices A, B, C, and D in order, then the theorem states that:
\( |\overline{AC}|\cdot |\overline{BD}|=|\overline{AB}|\cdot |\overline{CD}|+|\overline{BC}|\cdot |\overline{AD}| \)
where the vertical lines denote the lengths of the line segments between the named vertices.
This relation may be verbally expressed as follows:
If a quadrilateral is inscribable in a circle then the product of the measures of its diagonals is equal to the sum of the products of the measures of the pairs of opposite sides.
Moreover, the converse of Ptolemy's theorem is also true:
In a quadrilateral, if the sum of the products of its two pairs of opposite sides is equal to the product of its diagonals, then the quadrilateral can be inscribed in a circle.
Examples
Equilateral triangle
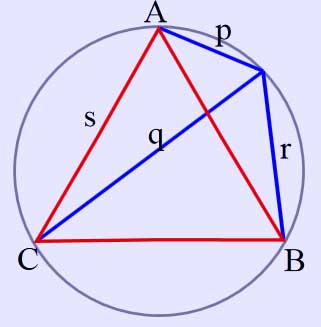
Equilateral triangle
Ptolemy's Theorem yields as a corollary a pretty theorem [2] regarding an equilateral triangle inscribed in a circle.
Given An equilateral triangle inscribed on a circle and a point on the circle.
The distance from the point to the most distant vertex of the triangle is the sum of the distances from the point to the two nearer vertices.
Proof: Follows immediately from Ptolemy's theorem:
\( qs=ps+rs\Rightarrow q=p+r. \)
Square
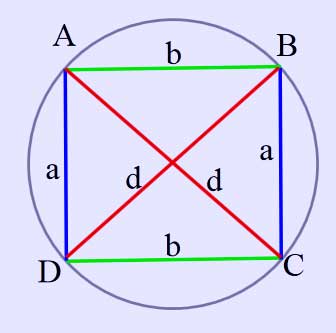
Any square can be inscribed in a circle whose center is the barycenter of the square. If the common length of its four sides is equal to a then the length of the diagonal is equal to a\sqrt{2} according to the Pythagorean theorem and the relation obviously holds.
Rectangle
Pythagoras' theorem: "manifestum est": Copernicus
More generally, if the quadrilateral is a rectangle with sides a and b and diagonal d then Ptolemy's theorem reduces to the Pythagorean theorem. In this case the center of the circle coincides with the point of intersection of the diagonals. The product of the diagonals is then d2, the right hand side of Ptolemy's relation is the sum a2 + b2.
Copernicus − who used Ptolemy's theorem extensively in his trigonometrical work − refers to this result as a 'Porism' or self evident corollary:
Furthermore it is clear (manifestum est) that when the chord subtending an arc has been given, that chord too can be found which subtends the rest of the semicircle.
De Revolutionibus Orbium Coelestium: Page 37. See last two lines of this page.
Nor for that matter does Copernicus refer to "Ptolemy's Theorem" but labels it more simply as "Theorema Secundum".
Pentagon
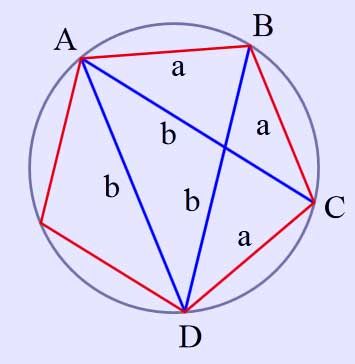
The golden ratio follows from this application of Ptolemy's theorem
A more interesting example is the relation between the length a of the side and the (common) length b of the 5 chords in a regular pentagon. In this case the relation reads b2 = a2 + ab which yields the golden ratio
\( \varphi = {b \over a} = {{1+\sqrt{5}}\over 2}. \) [3]
Side of decagon
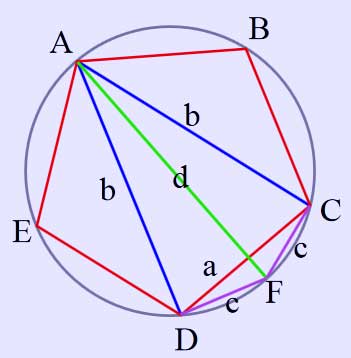
Side of the inscribed decagon
If now diameter AF is drawn bisecting DC so that DF and CF are sides c of an inscribed decagon, Ptolemy's Theorem can again be applied – this time to cyclic quadrilateral ADFC with diameter d as one of its diagonals:
\( ad=2bc\; \)
\( \Rightarrow ad=2\varphi ac \) where \( \varphi \) is the golden ratio.
\( \Rightarrow c=\frac{d}{2\varphi} \).[4]
whence the side of the inscribed decagon is obtained in terms of the circle diameter. Pythagoras' Theorem applied to right triangle AFD then yields "b" in terms of the diameter and "a" the side of the pentagon [5] is thereafter calculated as
\( a=\frac {b} {\varphi}=b(\varphi-1).\ \)
As Copernicus (following Ptolemy) wrote,
"The diameter of a circle being given, the sides of the triangle, tetragon, pentagon, hexagon and decagon, which the same circle circumscribes, are also given." – De Revolutionibus Orbium Coelestium: Liber Primus: Theorema Primum
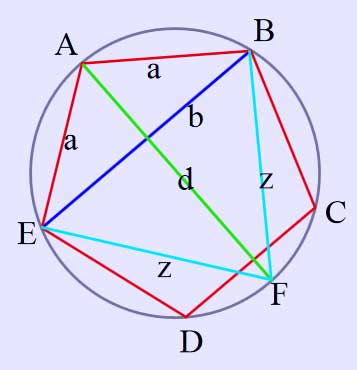
Complement of pentagon chord
Complement of the pentagon chord
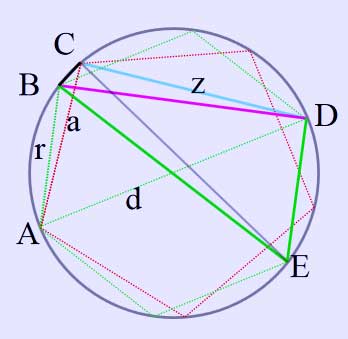
The ancient geometers are not done yet, for if the fifth vertex of the pentagon is marked as E and FE and BF are joined (with FE=BF=z), then cyclic quadrilateral EFBA will be formed with diagonals length d (diameter) and b.[6] Applying the 'Almagest' theorem yet again:
\( db=2az\; \)
\( \Rightarrow \varphi ad=2az \) where \( \varphi \) is the golden ratio.
\( \Rightarrow z=\frac{\varphi d} {2} \).
z subtends 540 at the circumference, c (the side of the decagon) subtends 180 at the circumference and thereby is established:
\( \sin(54^\circ)=\frac {\varphi}{2} \) and \( \sin(18^\circ)=\frac{1}{2\varphi}=\frac {\varphi-1}{2} \).
And since angle ABF is subtended by the diameter and is therefore right, the side of the pentagon is calculated by an even simpler route:
\( \sin(36^\circ)=\frac {\sqrt{3-\varphi}}{2}\text{ and }\sin(72^\circ)=\frac{\sqrt{2+\varphi}}{2}. \)
Based on his circle of diameter 200000 units, Copernicus provides accurate numerical values for the four pentagon related chords corresponding to these angles:
"Since the side of the decagon which subtends 360 has been shown to have 61803 parts, whereof the diameter has 200000 parts – the chord which subtends the remaining 1440 of the semicircle has 190211 parts. And in the case of side of the pentagon, which is equal to 117557 parts of the diameter and subtends an arc of 720, a straight line of 161803 parts is given, and it subtends the remaining 1080 of the circle".
Golden ratio aficionados will instantly recognize the digits 161803 and 61803 as corresponding to \varphi and its reciprocal.[7] The chords are of considerable historical importance because, along with the sides of the triangle and tetragon (square), they enable the generation of a table of half chords (effectively sine values) [8] which in turn underpins many of the key astronomical measurements and calculations effected by Copernicus in the development of his helio-centric model:
"Because the proofs which we shall use in almost the entire work deal with straight lines and arcs, with plane and spherical triangles and because Euclid's Elements, although they clear up much of this, do not have what is here most required, namely, how to find the sides from angles and the angles from the sides ... there has accordingly been found a method whereby the lines subtending any arc may be known."
Euclid 13:10
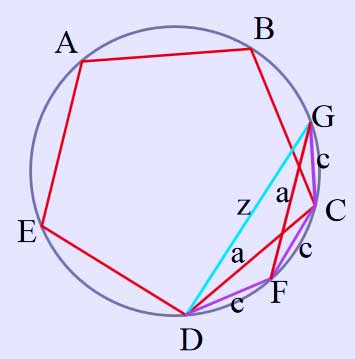
Square of Pentagon chord equals sum of squares of decagon and hexagon chords
Next our attention is drawn to point G midway between points B and C on the circumference. CG, FG and DG are joined forming cyclic quadrilateral DFCG in which three sides belong to the regular decagon (length c) and the fourth DG is of length z. Diagonals DC and FG are both of length a (side of the pentagon) Then:
\( c^2+cz=a^2\; \)
Therefore
\( \begin{align} c^2+\frac{d}{2 \varphi}\frac{\varphi d}{2} & = a^2, \\[8pt] c^2+\frac{d^2}{4} & = a^2, \\[8pt] c^2+r^2 & = a^2, \end{align} \)
where r is the radius of the circle and also the side of the inscribed hexagon.
Whence with relative ease is proved Proposition 10 in Book XIII of Euclid's Elements: The square on the side of the pentagon equals the sum of the squares on the sides of the hexagon and the decagon inscribed in the same circle.
In modern trigonometric notation this corresponds to the identity:
\( \sin^2(18^\circ)+\sin^2(30^\circ)=\sin^2(36^\circ)\; \)
The Pythagorean nature of this relationship makes possible the construction of a regular pentagon as demonstrated here.
Theorema Tertium
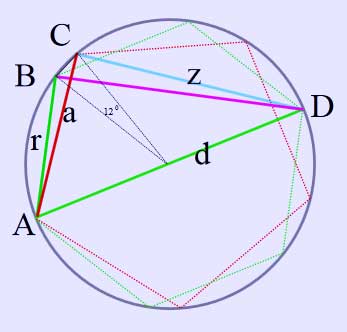
Determination of the chord subtending 12 degrees of arc
A well documented classical application of the "Second Theorem" as illustrated in the diagram is the determination of chord BC subtending 12 degrees of arc. Referring to the diagram:
\( \begin{align} \overline{BC} & = \frac{\overline{BD}\cdot\overline{AC}-\overline{AB}\cdot\overline{CD}}{\overline{AD}} \\[8pt] & = \frac{\sqrt{3}ra-rz}{2r} \\[8pt] & = \frac{a\sqrt{3}-z}{2}. \end{align} \)
"When, for example, the sides of the pentagon and hexagon are given from the above, by this computation a line is given subtending 120 which is the difference between the arcs − and it is equal to 20905 parts of the diameter." De Revolutionibus Orbium Coelestium: Liber Primus: Theorema Tertium
Based on his circle of diameter 200000 units and already established chords of pentagon, hexagon and triangle the calculation effected by Copernicus would have been:
\( \frac{173205\times117557-100000\times161803}{200000}\approx20906. \)
A small rounding error is evident in the result but the corresponding entry (in the Copernican table of half chords ) of 10453 units against 6 degrees is correct as may readily be verified on a calculator (sin 6).
In modern trigonometric notation, the above calculation corresponds to the following application of a compound angle formula:
\( \sin(6^\circ)=\sin(36^\circ)\cos(30^\circ)-\cos(36^\circ)\sin(30^\circ). \, \)
Theorema Quintum
Determination of the chord subtending a sum of arcs
The previous diagram demonstrated a general technique for calculating the chord subtending the difference between two arcs. The following diagram neatly reverses this procedure to obtain the chord subtending the sum of arcs: ie determination of chord AC given chords AB and BC.
Compared with the previous we note that diameter BE has been swung across from point B to point E. EC and ED are joined. Since AEDB is a rectangle DE=AB. Thus in cyclic quadrilateral BEDC, sides BE, BC and ED are known along with diagonals CE and BD by application of the "Porism" (Pythagoras Thm). Then:
\( \overline{CD}=\frac{\overline{EC}\cdot\overline{BD}-\overline{ED}\cdot\overline{BC}}{\overline{BE}}. \)
In the specific example illustrated in the diagram, calculation of chord CD in cyclic quadrilateral BEDC corresponds to the following application of a compound angle formula:
\( \cos(30^\circ+6^\circ)=\sin(60^\circ-6^\circ)=\sin(60^\circ)\cos(6^\circ)-\cos(60^\circ)\sin(6^\circ). \)
The required chord AC (in this example corresponding to sin(30+6)) is then calculated by application of the "Porism".
De Revolutionibus Orbium Coelestium: Liber Primus: Theorema Quintum
Other polygons
When applied repeatedly, Ptolemy's theorem allows one to compute the lengths of all diagonals for polygons inscribed in a circle with vertices P1, ..., Pn, if the sides are given together with all the length values of the "next to sides" chords connecting two vertices Pi and Pi+2 (with indices taken modulo n).
Proofs
Geometric proof
Constructions for a proof of Ptolemy's theorem
Let ABCD be a cyclic quadrilateral.
Note that on the chord BC, the inscribed angles ∠BAC = ∠BDC, and on AB, ∠ADB = ∠ACB.
Construct K on AC such that ∠ABK = ∠CBD;
Note that since ∠ABK + ∠CBK = ∠ABC = ∠CBD + ∠ABD, ∠CBK = ∠ABD.
Now, by common angles △ABK is similar to △DBC, and likewise △ABD is similar △KBC.
Thus AK/AB = CD/BD, and CK/BC = DA/BD;
Thus AK·BD = AB·CD, and CK·BD = BC·DA;
By adding equality: AK·BD + CK·BD = AB·CD + BC·DA;
Thus by factorizing: (AK+CK)·BD = AB·CD + BC·DA;
But AK+CK = AC, so AC·BD = AB·CD + BC·DA; Q.E.D.
Note that the proof is clearly only valid for simple cyclic quadrilaterals; if the quadrilateral is complex then K will be located outside the line segment AC, so AK−CK=±AC, giving the expected result.
Trigonometric proof
It suffices to prove the theorem for the standard unit circle (the statement of the theorem is invariant under re-scaling and translation). Introducing polar coordinates one may represent the four vertices \( \,P_1, \ldots,P_4\, \) in the form
\( P_i=(\,\cos\alpha_i,\sin\alpha_i \,)\text{ where }\alpha_i \in \,[\,0,2\pi).\, \)
After a possible renumbering of the Pi one can also assume that the four vertices appear in natural counterclockwise order which means that \( \,\alpha_1 < \alpha_2 < \alpha_3 <\alpha_4\,. \)
A basic result from trigonometry states that for two points \( x=(\,\cos\alpha,\sin\alpha \,) \) and \( y=(\,\cos\beta,\sin\beta\,) \) on the unit circle written in polar coordinates their Euclidean distance ||x − y|| is given as
\( ||x-y||=2\sin\left({{|\alpha-\beta|}\over 2}\right). \)
If \( (P_i,P_j),\;\; i<j \) is an (ordered) pair of vertices of the given quadrilateral this formula implies
\( \overline{P_i P_j}=2\sin\left({\alpha_j\over 2}-{\alpha_i \over 2}\right). \)
Ptolemy's relation
\( \overline{P_1P_3}\cdot \overline{P_2P_4}=\overline{P_1P_2}\cdot \overline{P_3P_4}+\overline{P_1P_4}\cdot \overline{P_2P_3} \)
then follows from the quadratic addition relation
\( \sin(\theta_3-\theta_1) \sin(\theta_4-\theta_2) = \sin(\theta_2-\theta_1)\sin(\theta_4-\theta_3) + \sin(\theta_4-\theta_1)\sin(\theta_3-\theta_2)\, \)
satisfied by the sine-function which in turn can be deduced from the trigonometric identity (which is the products-to-sum identity for the sine)
\( \sin\alpha\sin\beta={1\over2} \left( \cos(\alpha-\beta)-\cos(\alpha+\beta)\right) \)
applied to each of the three products of sines (the resulting six terms cancel out in pairs).
Concluding remark (explaining the naming "addition relation"):
If one introduces the difference angles \( \,\delta_i=\theta_{i+1}-\theta_{i}\, for \,i=1, \ldots,3\, \) then the relation
\( \sin(\theta_3-\theta_1)\sin(\theta_4-\theta_2) = \sin(\theta_2-\theta_1)\sin(\theta_4-\theta_3) + \sin(\theta_4-\theta_1)\sin(\theta_3-\theta_2)\, \)
turns into
\( \sin(\delta_1 +\delta_2 )\sin(\delta_2 +\delta_3 ) = \sin(\delta_1)\sin(\delta_3) + \sin(\delta_1+\delta_2+\delta_3)\sin(\delta_2). \, \)
Solving for \( \sin(\delta_1+\delta_2+\delta_3\,) \), this relation may be interpreted as a "triple" addition relation expressing the sine of a triple angle sum \,\delta_1+\delta_2+\delta_3\, as a rational expression in the sine values \sin(\delta_i+\delta_j\,) and \sin \,\delta_i\,. Written out explicitly:
\( \sin(\delta_1+\delta_2+\delta_3) = {{\sin(\delta_1 +\delta_2 )\sin(\delta_2 +\delta_3) - \sin(\delta_1)\sin(\delta_3)}\over {\sin\delta_2}}. \)
Proof using the law of sines
Ptolemy's Theorem
The proof which follows is substantively similar to the previous but adopts a different methodology and concludes with an interestingly symmetric formula for the product of diagonals and sum of products of opposite sides.
Preliminary observations and identities
In the diagram sides AB,BC,CD and DA are labelled \( S_1,S_2,S_3\, \) and \( S_4\, \) and subtend angles \( \theta_1,\theta_2,\theta_3\ \), and \( \theta_4\ \), respectively. Applying sum of angles in triangle ABC it should be noted that \( \theta_1+\theta_2+\theta_3+\theta_4=180^\circ\, \). Therefore the sum of any two angles is supplementary with the sum of the other two and any single angle is supplementary with the sum of the other three. In general for supplementary angles x and y:
\( \begin{align} \sin(x)&=\sin(y)\\ \cos(x)&=-\cos(y).\\ \end{align} \)
We will also need the identity \( \cos(\theta_i-\theta_j)=\cos(\theta_j-\theta_i)\ \), and the following product to sum identity:
\( \sin(x)\sin(y)=\frac{\cos(x-y)-\cos(x+y)}{2}. \)
Proof
Apply the sine rule to triangles ABC, ADC and ABD within their common circumscribing circle ABCD with radius R:
\( \frac{S_1}{\sin\theta_1}=\frac{S_2}{\sin\theta_2}=\frac{S_3}{\sin\theta_3}=\frac{S_4}{\sin\theta_4} = \frac{\overline{AC}}{\sin(\theta_3+\theta_4)}=\frac{\overline{BD}}{\sin(\theta_3+\theta_2)}=2R. \)
From this we obtain:
\( \begin{align} S_1S_3+S_2S_4 & = 4R^2(\sin\theta_1\sin\theta_3+\sin\theta_2\sin\theta_4)\\ & = 2R^2[\cos(\theta_1-\theta_3)-\cos(\theta_1+\theta_3)-\cos(\theta_2+\theta_4)+\cos(\theta_2-\theta_4)]\\ & = 2R^2[\cos(\theta_1-\theta_3)+\cos(\theta_2-\theta_4)]. \end{align} \)
The product to sum identity has been applied twice and the middle two terms cancel out on account of being cosines of supplementary angles.
Similarly we can obtain an expression for the product of diagonals:
\( \begin{align} \overline{BD} \cdot\overline{AC} & = 4R^2[\sin(\theta_3+\theta_2)\sin(\theta_3+\theta_4)]\\ & = 2R^2[\cos(\theta_2-\theta_4)-\cos(2\theta_3+\theta_4+\theta_2)]\\ & = 2R^2[\cos(\theta_2-\theta_4)+\cos(\theta_1-\theta_3)]. \end{align} \)
Once again the product to sum identity has been applied and the second term has been rewritten in terms of its supplementary angle.
We may now present Ptolemy's theorem with an addendum by way of the "marrying formula" for product of diagonals and sum of products of opposite sides:
\( S_1S_3+S_2S_4=\overline{AC} \cdot\overline{BD} =2R^2[\cos(\theta_2-\theta_4)+\cos(\theta_1-\theta_3)]\; \)
where R is the radius of the circumscribing circle and \( \theta_1,\theta_2,\theta_3,\theta_4\, \) are the angles subtended by sides \( S_1,S_2,S_3,S_4\ \), respectively.
In the case of a circle of unit diameter, Ptolemy's theorem can be written in trigonometric form as follows:
\( \sin\theta_1\sin\theta_3+\sin\theta_2\sin\theta_4=\sin(\theta_3+\theta_2)\sin(\theta_3+\theta_4).\; \)
Algebraic proof
An alternative proof can be given using complex number calculus and projective analytic geometry, introducing complex coordinates for the vertices of the quadrilateral. Again it suffices to prove the theorem for the standard unit circle \( S^1=\{z \in \mathbb{C}, \; z\overline{z}=1\} \).
Ptolemy's Relation
\( \overline{P_1P_3}\cdot \overline{P_2P_4}=\overline{P_1P_2}\cdot \overline{P_3P_4}+\overline{P_1P_4}\cdot \overline{P_2P_3} \)
can be reformulated as
\( {{\overline{P_1P_3}\cdot \overline{P_2P_4}}\over{\overline{P_1P_4}\cdot \overline{P_2P_3}}} =1+{{\overline{P_1P_2}\cdot \overline{P_3P_4}}\over{\overline{P_1P_4}\cdot \overline{P_2P_3}}} \ . \)
Written in this form Ptolemy's theorem is in fact a "disguised" form of the relation
\( \,\operatorname{cr}(z_1,z_2,z_3,z_4)=1- \operatorname{cr}(z_1,z_3,z_2,z_4) \)
valid for the cross-ratio \( \,\operatorname{cr}(z_1,z_2,z_3,z_4)={{(z_1-z_3)(z_2-z_4)}\over{(z_1-z_4)(z_2-z_3)}} \) of any four (pairwise different) complex numbers \( z_1,\ldots,z_4. \)
To make this connection explicit one represents the four vertices \( P_1, \ldots, P_4 \) as four complex numbers z_1, \ldots, z_4 of norm one, arranged in (counterclockwise) cyclic order on the unit circle. For two complex numbers x,y on the unit circle their squared distance equals
\( |x-y|^2=(x-y)\cdot(\overline{x}-\overline{y}) = (x-y)\cdot\left({1\over x}-{1\over y}\right) = -{(x-y)^2\over{xy}} \ .\)
Therefore for any quadruple of (pairwise different) complex numbers (z_1,z_2,z_3,z_4) on the unit circle the square of the "length cross-ratio"
\( {{|z_1-z_3|\cdot |z_2-z_4|}\over{|z_1-z_4|\cdot |z_2-z_3|}} \)
is equal to the square \( \,\operatorname{cr}^2(z_1,z_2,z_3,z_4) \) of the ordinary ("complex points" ) cross-ratio \( \,{{(z_1-z_3)(z_2-z_4)}\over{(z_1-z_4)(z_2-z_3)}} \). Taking square roots one first deduces
\( {{|z_1-z_3|\cdot |z_2-z_4|}\over{|z_1-z_4|\cdot |z_2-z_3|}}=\epsilon {{(z_1-z_3)(z_2-z_4)}\over{(z_1-z_4)(z_2-z_3)}}=\epsilon\, \operatorname{cr}( z_1,z_2,z_3,z_4) \)
for any quadruple \( \,(z_1,\ldots,z_4) \) of points on the unit circle. The sign factor \epsilon \in \{ -1,1\} depends on the relative position of the four points \( \,z_1, \ldots, z_4 \) on the unit circle and can be determined using the invariance of the cross-ratio under a linear fractional transformation z \mapsto {{az+b}\over{cz+d}}. Assume that the quadruple \( \,(z_1, \ldots,z_4) \) on the unit circle is arranged in natural (counterclockwise) cyclic order. Then
\( \,\operatorname{cr}(z_1,z_2,z_3,z_4)>1. \)
This property can be proved using the projective transformation \( r:\; z \mapsto i{{(1+z)}\over{(1-z)}} \) (which is the "inverse Cayley transform"). It maps the punctured unit circle \( S^1\setminus \{z=1\} \) (continuously) to the real line \( \mathbb{R} \) (with the upper (resp. lower) arc of the unit circle mapping to the negative (resp. positive) half-line). In polar coordinates the map is given as \( \,r(e^{ i \alpha})=-\cot( \alpha /2) \) which shows that it defines a monotone function in the "angle" coordinate \( \alpha \in )0,2\pi( \). Therefore the sign of the cross-ratio can be read off from the mutual order of the image points on the real line. After multiplying the \( z_i \) with a suitable scalar z' of norm 1 one may in addition assume that z_i \ne 1 for all i. If the quadruple \( (\,z_1, \ldots,z_4) \) on the unit circle (punctured at z=1) is arranged in natural (counterclockwise) cyclic order the image quadruple \( \,(y_1, \ldots, y_4):=(\,r(z_1),r(z_2),r(z_3),r(z_4)\,) \) satisfies \( \, y_1 <y_2 <y_3<y_4 \) . The relation
\( \operatorname{cr}(y_1,y_2,y_3,y_4)-1={{(y_1-y_3)(y_2-y_4)}\over{(y_1-y_4)(y_2-y_3)}} -1={{(y_1-y_2)(y_3-y_4)}\over{(y_1-y_4)(y_2-y_3)}}>0 \)
then shows that \( \,\operatorname{cr}(z_1,z_2,z_3,z_4)=\operatorname{cr}(y_1,y_2,y_3,y_4)>1 \). On the other hand, if one interchanges the middle pair (z_2,z_3) in a cyclically ordered quadruple then the cross-ratio will become negative because \( \,\operatorname{cr}(z_1,z_3,z_2,z_4)=1-\operatorname{cr}(z_1,z_2,z_3,z_4)<0 \), using the relation of cross-ratios
\( {{(z_1-z_3)(z_2-z_4)}\over{(z_1-z_4)(z_2-z_3)}}=1-{{(z_1-z_2)(z_3 -z_4)}\over{(z_1-z_4)(z_3-z_2)}}.\, \)
Summarizing the sign discussion one obtains that for a quadruple (z_1, \ldots, z_4) of (pairwise different) points on the unit circle given in (counterclockwise) cyclic order one has
\( {{|z_1-z_3|\cdot |z_2-z_4|}\over{|z_1-z_4|\cdot |z_2-z_3|}}=+{{(z_1-z_3)(z_2-z_4)}\over{(z_1-z_4)(z_2-z_3)}} \)
and
\( {{|z_1-z_2|\cdot |z_3-z_4|}\over{|z_1-z_4|\cdot |z_3-z_2|}}=-{{(z_1-z_2)(z_3-z_4)}\over{(z_1-z_4)(z_3-z_2)}}.\, \)
Ptolemy's relation
\( {{\overline{P_1P_3}\cdot \overline{P_2P_4}}\over{\overline{P_1P_4}\cdot \overline{P_2P_3}}} =1+{{\overline{P_1P_2}\cdot \overline{P_3P_4}}\over{\overline{P_1P_4}\cdot \overline{P_2P_3}}} \)
can now be interpreted as the algebraic relation (already used above) between cross-ratios
\( {{(z_1-z_3)(z_2-z_4)}\over{(z_1-z_4)(z_2-z_3)}}=1-{{(z_1-z_2)(z_3 -z_4)}\over{(z_1-z_4)(z_3-z_2)}} \)
using the representation of the vertices \( P_1,\ldots,P_4 \) as the points z_1, \ldots, z_4 on the unit circle.
Corollaries
Corollary 1: Pythagoras' Theorem
In the case of a circle of unit diameter the sides \( S_1,S_2,S_3,S_4\ \); of any cyclic quadrilateral ABCD are numerically equal to the sines of the angles \theta_1,\theta_2,\theta_3\, and \theta_4\, which they subtend. Similarly the diagonals are equal to the sine of the sum of whichever pair of angles they subtend. We may then write Ptolemy's Theorem in the following trigonometric form:
\( \sin\theta_1\sin\theta_3+\sin\theta_2\sin\theta_4=\sin(\theta_1+\theta_2)\sin(\theta_3+\theta_4)\; \)
Applying certain conditions to the subtended angles \( \theta_1,\theta_2,\theta_3\ \), and \( \theta_4\ \), it is possible to derive a number of important corollaries using the above as our starting point. In what follows it is important to bear in mind that the sum of angles \( \theta_1+\theta_2+\theta_3+\theta_4=180^\circ\,. \)
Corollary 1. Pythagoras' theorem
Let \( \theta_1=\theta_3\; and \theta_2=\theta_4\ \);. Then \( \theta_1+\theta_2=\theta_3+\theta_4=90^\circ\ \); (since opposite angles of a cyclic quadrilateral are supplementary). Then:[9]
\( \sin\theta_1\sin\theta_3+\sin\theta_2\sin\theta_4=\sin(\theta_1+\theta_2)\sin(\theta_3+\theta_4) \, \)
\( \sin^2\theta_1+\sin^2\theta_2=\sin^2(\theta_1+\theta_2) \, \)
\( \sin^2\theta_1+\cos^2\theta_1=1 \, \)
Corollary 2. The law of cosines
Corollary 2: The Law of Cosines
Let \( \theta_2=\theta_4\ \);. The rectangle of corollary 1 is now a symmetrical trapezium with equal diagonals and a pair of equal sides. The parallel sides differ in length by 2x units where:
\( x=S_2\cos(\theta_2+\theta_3)\; \)
It will be easier in this case to revert to the standard statement of Ptolemy's theorem:
\( \begin{array}{lcl}\\ S_1 S_3 +S_2 S_4=\overline{AC}\cdot\overline{BD}\\ \Rightarrow S_1 S_3+S_2^2=\overline{AC}^2\\ \Rightarrow S_1[S_1-2S_2\cos(\theta_2+\theta_3)]+S_2^2=\overline{AC}^2\\ \Rightarrow S_1^2+S_2^2-2S_1S_2\cos(\theta_2+\theta_3)=\overline{AC}^2\\ \end{array} \)
The cosine rule for triangle ABC.
Corollary 3: Compound angle sine (+)
Let
\( \theta_1+\theta_2=\theta_3+\theta_4=90^\circ. \; \)
Then
\( \sin\theta_1\sin\theta_3+\sin\theta_2\sin\theta_4=\sin(\theta_3+\theta_2)\sin(\theta_3+\theta_4) \)
Therefore
\( \cos\theta_2\sin\theta_3+\sin\theta_2\cos\theta_3=\sin(\theta_3+\theta_2)\times 1 \, \)
Formula for compound angle sine (+).[10]
Corollary 4: Compound angle sine (−)
Let \theta_1=90^\circ. Then \theta_2+(\theta_3+\theta_4)=90^\circ \). Hence,
\( \sin\theta_1\sin\theta_3+\sin\theta_2\sin\theta_4=\sin(\theta_3+\theta_2)\sin(\theta_3+\theta_4) \, \)
\( \sin\theta_3+\sin\theta_2\cos(\theta_2+\theta_3)=\sin(\theta_3+\theta_2)\cos\theta_2 \, \)
\( \sin\theta_3=\sin(\theta_3+\theta_2)\cos\theta_2-\cos(\theta_2+\theta_3)\sin\theta_2 \, \)
Formula for compound angle sine (−).[10]
This derivation corresponds to the Third Theorem as chronicled by Copernicus following Ptolemy in Almagest. In particular if the sides of a pentagon (subtending 36° at the circumference) and of a hexagon (subtending 30° at the circumference) are given, a chord subtending 6° may be calculated. This was a critical step in the ancient method of calculating tables of chords.[11]
Corollary 5: Compound angle cosine (+)
This corollary is the core of the Fifth Theorem as chronicled by Copernicus following Ptolemy in Almagest.
Let \( \theta_3=90^\circ \). Then \( \theta_1+(\theta_2+\theta_4)=90^\circ \). Hence
\( \sin\theta_1\sin\theta_3+\sin\theta_2\sin\theta_4=\sin(\theta_3+\theta_2)\sin(\theta_3+\theta_4) \, \)
\( \cos(\theta_2+\theta_4)+\sin\theta_2\sin\theta_4=\cos\theta_2\cos\theta_4 \, \)
\( \cos(\theta_2+\theta_4)=\cos\theta_2\cos\theta_4-\sin\theta_2\sin\theta_4 \, \)
Formula for compound angle cosine (+)
Despite lacking the dexterity of our modern trigonometric notation, it should be clear from the above corollaries that in Ptolemy's theorem (or more simply the Second Theorem) the ancient world had at its disposal an extremely flexible and powerful trigonometric tool which enabled the cognoscenti of those times to draw up accurate tables of chords (corresponding to tables of sines) and to use these in their attempts to understand and map the cosmos as they saw it. Since tables of chords were drawn up by Hipparchus three centuries before Ptolemy, we must assume he knew of the 'Second Theorem' and its derivatives. Following the trail of ancient astronomers, history records the star catalogue of Timocharis of Alexandria. If, as seems likely, the compilation of such catalogues required an understanding of the 'Second Theorem' then the true origins of the latter disappear thereafter into the mists of antiquity but it cannot be unreasonable to presume that the astronomers, architects and construction engineers of ancient Egypt may have had some knowledge of it.
Ptolemy's inequality
This is not a cyclic quadrilateral. The equality never holds here, and is unequal in the direction indicated by Ptolemy's inequality.
The equation in Ptolemy's theorem is never true with non-cyclic quadrilaterals. Ptolemy's inequality is an extension of this fact, and it is a more general form of Ptolemy's theorem. It states that, given a quadrilateral ABCD, then
\( \overline{AB}\cdot \overline{CD}+\overline{BC}\cdot \overline{DA} \ge \overline{AC}\cdot \overline{BD} \)
where equality holds if and only if the quadrilateral is cyclic. This special case is equivalent to Ptolemy's theorem.
See also
Golden ratio
Casey's theorem
Notes
^ C. Ptolemy, Almagest, Book 1, Chapter 10.
^ Wilson, Jim. "Ptolemy's Theorem." link verified 2009-04-08
^ Proposition 8 in Book XIII of Euclid's Elements proves by similar triangles the same result: namely that length a (the side of the pentagon) divides length b (joining alternate vertices of the pentagon) in "mean and extreme ratio".
^ And in analogous fashion Proposition 9 in Book XIII of Euclid's Elements proves by similar triangles that length c (the side of the decagon) divides the radius in "mean and extreme ratio".
^ An interesting article on the construction of a regular pentagon and determination of side length can be found at the following reference [1]
^ The Pentagon and Trigonometry illuminates another means whereby the ancients may have reached an understanding of the golden ratio and chords of the pentagon.
^ Copernicus cites Euclid XIII.5 and XIII.9 for his determination of the decagon chord and the somewhat ponderous XIII.10 for the pentagon chord. The remaining pair of chords were calculated using the "Porism" now referred to as Pythagoras' Theorem. No doubt the great astronomer was aware of the simpler derivations employing the "Second Theorem" but may have prudently opted to cite 'approved' sources where possible.
^ Given the unit circle with sector ABO subtending an arc of \( 2\theta^\circ \), we may write \( \sin(\theta)=\frac{1}{2}\mathrm{chord}(2\theta) \)− a relationship expressed in words by Copernicus:
Nevertheless I think it will be enough if in the table we give only the halves of the chords subtending twice the arc, whereby we may concisely comprehend in the quadrant what it used to be necessary to spread out over the semicircle.
^ In De Revolutionibus Orbium Coelestium, Copernicus does not refer to Pythagoras' Theorem by name but uses the term 'Porism' – a word which in this particular context would appear to denote an observation on – or obvious consequence of – another existing theorem. The 'Porism' can be viewed on pages 36 and 37 of DROC (Harvard electronic copy)
^ a b "Sine, Cosine, and Ptolemy's Theorem".
^ To understand the Third Theorem, compare the Copernican diagram shown on page 39 of the Harvard copy of De Revolutionibus to that for the derivation of sin(A-B) found in the above cut-the-knot web page
References
Coxeter, H. S. M. and Greitzer, S. L.: "Ptolemy's Theorem and its Extensions." §2.6 in Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 42–43, 1967.
De Revolutionibus Orbium Coelestium, Copernicus, Nicolaus. English translation from On the Shoulders of Giants, Hawking, S 2002, Penguin Books. ISBN 0-14-101571-3
External links
Proof of Ptolemy's Theorem for Cyclic Quadrilateral
MathPages − On Ptolemy's Theorem
Elert, Glenn (1994). "Ptolemy's Table of Chords". E-World.
Ptolemy's Theorem at cut-the-knot
Compound angle proof at cut-the-knot
Ptolemy's Theorem on PlanetMath
Ptolemy Inequality on MathWorld
De Revolutionibus Orbium Coelestium at Harvard.
Deep Secrets: The Great Pyramid, the Golden Ratio and the Royal Cubit
Ptolemy's Theorem by Jay Warendorff, The Wolfram Demonstrations Project.
Book XIII of Euclid's Elements
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

