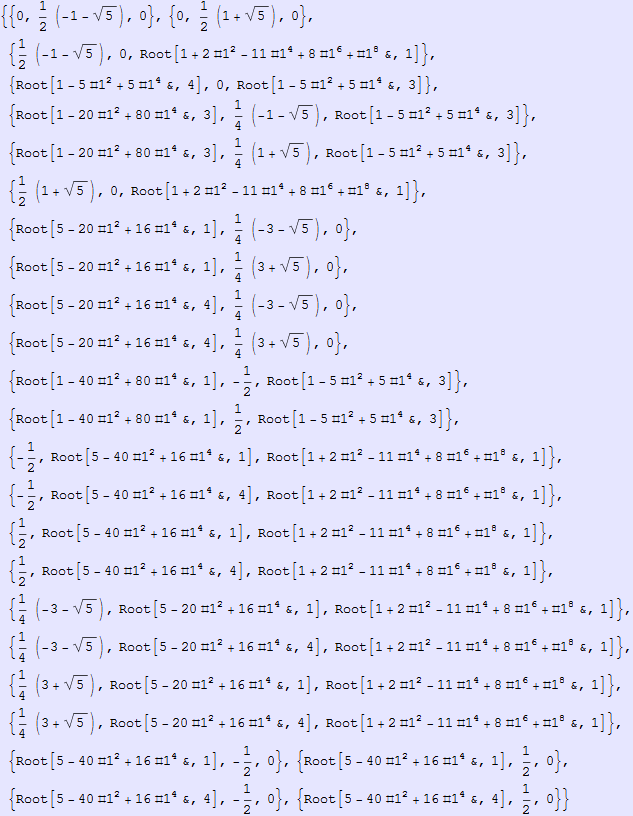In[554]:=
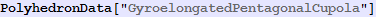
Out[554]=
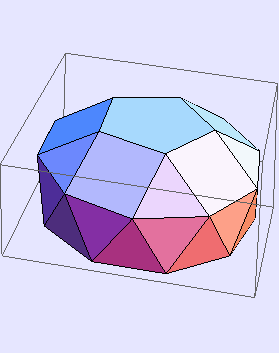
In[555]:=
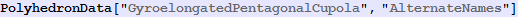
Out[555]=
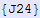
In[556]:=

Out[556]=
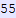
In[557]:=
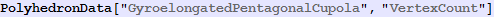
Out[557]=
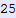
In[558]:=

Out[558]=
In[559]:=
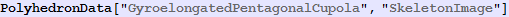
Out[559]=
In[560]:=

Out[560]=
In[561]:=
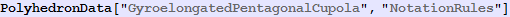
Out[561]=
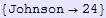
In[562]:=

Out[562]//InputForm=
Graphics3D[GraphicsComplex[
{{0, (-1 - Sqrt[5])/2, -Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 -
265545895321600*#1^3 - 3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 +
3030095233024000*#1^7 + 3583731197542400*#1^8 & , 1, 0]},
{0, (1 + Sqrt[5])/2, -Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 -
265545895321600*#1^3 - 3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 +
3030095233024000*#1^7 + 3583731197542400*#1^8 & , 1, 0]},
{(-1 - Sqrt[5])/2, 0, Root[1 + 2*#1^2 - 11*#1^4 + 8*#1^6 + #1^8 & , 1, 0] -
Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {Root[1 - 5*#1^2 + 5*#1^4 & , 4, 0], 0,
Root[1 - 5*#1^2 + 5*#1^4 & , 3, 0] - Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 -
265545895321600*#1^3 - 3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 +
3030095233024000*#1^7 + 3583731197542400*#1^8 & , 1, 0]}, {Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0],
(-1 - Sqrt[5])/4, Root[1 - 5*#1^2 + 5*#1^4 & , 3, 0] -
Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {Root[1 - 20*#1^2 + 80*#1^4 & , 3, 0], (1 + Sqrt[5])/4,
Root[1 - 5*#1^2 + 5*#1^4 & , 3, 0] - Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 -
265545895321600*#1^3 - 3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 +
3030095233024000*#1^7 + 3583731197542400*#1^8 & , 1, 0]},
{(1 + Sqrt[5])/2, 0, Root[1 + 2*#1^2 - 11*#1^4 + 8*#1^6 + #1^8 & , 1, 0] -
Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {Root[5 - 20*#1^2 + 16*#1^4 & , 1, 0], (-3 - Sqrt[5])/4,
-Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {Root[5 - 20*#1^2 + 16*#1^4 & , 1, 0], (3 + Sqrt[5])/4,
-Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {Root[5 - 20*#1^2 + 16*#1^4 & , 4, 0], (-3 - Sqrt[5])/4,
-Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {Root[5 - 20*#1^2 + 16*#1^4 & , 4, 0], (3 + Sqrt[5])/4,
-Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {Root[1 - 40*#1^2 + 80*#1^4 & , 1, 0], -1/2,
Root[1 - 5*#1^2 + 5*#1^4 & , 3, 0] - Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 -
265545895321600*#1^3 - 3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 +
3030095233024000*#1^7 + 3583731197542400*#1^8 & , 1, 0]}, {Root[1 - 40*#1^2 + 80*#1^4 & , 1, 0], 1/2,
Root[1 - 5*#1^2 + 5*#1^4 & , 3, 0] - Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 -
265545895321600*#1^3 - 3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 +
3030095233024000*#1^7 + 3583731197542400*#1^8 & , 1, 0]},
{-1/2, Root[5 - 40*#1^2 + 16*#1^4 & , 1, 0], Root[1 + 2*#1^2 - 11*#1^4 + 8*#1^6 + #1^8 & , 1, 0] -
Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {-1/2, Root[5 - 40*#1^2 + 16*#1^4 & , 4, 0],
Root[1 + 2*#1^2 - 11*#1^4 + 8*#1^6 + #1^8 & , 1, 0] -
Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {1/2, Root[5 - 40*#1^2 + 16*#1^4 & , 1, 0],
Root[1 + 2*#1^2 - 11*#1^4 + 8*#1^6 + #1^8 & , 1, 0] -
Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {1/2, Root[5 - 40*#1^2 + 16*#1^4 & , 4, 0],
Root[1 + 2*#1^2 - 11*#1^4 + 8*#1^6 + #1^8 & , 1, 0] -
Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {(-3 - Sqrt[5])/4, Root[5 - 20*#1^2 + 16*#1^4 & , 1, 0],
Root[1 + 2*#1^2 - 11*#1^4 + 8*#1^6 + #1^8 & , 1, 0] -
Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {(-3 - Sqrt[5])/4, Root[5 - 20*#1^2 + 16*#1^4 & , 4, 0],
Root[1 + 2*#1^2 - 11*#1^4 + 8*#1^6 + #1^8 & , 1, 0] -
Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {(3 + Sqrt[5])/4, Root[5 - 20*#1^2 + 16*#1^4 & , 1, 0],
Root[1 + 2*#1^2 - 11*#1^4 + 8*#1^6 + #1^8 & , 1, 0] -
Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {(3 + Sqrt[5])/4, Root[5 - 20*#1^2 + 16*#1^4 & , 4, 0],
Root[1 + 2*#1^2 - 11*#1^4 + 8*#1^6 + #1^8 & , 1, 0] -
Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {Root[5 - 40*#1^2 + 16*#1^4 & , 1, 0], -1/2,
-Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {Root[5 - 40*#1^2 + 16*#1^4 & , 1, 0], 1/2,
-Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {Root[5 - 40*#1^2 + 16*#1^4 & , 4, 0], -1/2,
-Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}, {Root[5 - 40*#1^2 + 16*#1^4 & , 4, 0], 1/2,
-Root[9607030429441 + 119077149816320*#1 + 412521362904960*#1^2 - 265545895321600*#1^3 -
3381046121123840*#1^4 - 2030856201830400*#1^5 + 6490210421964800*#1^6 + 3030095233024000*#1^7 +
3583731197542400*#1^8 & , 1, 0]}}, Polygon[{{19, 15, 17, 21, 7, 20, 16, 14, 18, 3}, {3, 18, 22},
{18, 14, 8}, {14, 16, 1}, {16, 20, 10}, {20, 7, 24}, {7, 21, 25}, {21, 17, 11}, {17, 15, 2}, {15, 19, 9},
{19, 3, 23}, {18, 8, 22}, {14, 1, 8}, {16, 10, 1}, {20, 24, 10}, {7, 25, 24}, {21, 11, 25}, {17, 2, 11},
{15, 9, 2}, {19, 23, 9}, {3, 22, 23}, {6, 13, 12, 5, 4}, {13, 6, 2, 9}, {12, 13, 23, 22}, {5, 12, 8, 1},
{4, 5, 10, 24}, {6, 4, 25, 11}, {11, 2, 6}, {9, 23, 13}, {22, 8, 12}, {1, 10, 5}, {24, 25, 4}}]]]
In[563]:=

Out[563]=
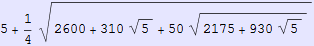
In[564]:=

Out[564]=
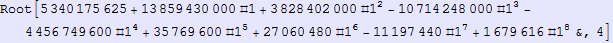
In[565]:=
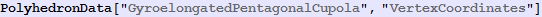
Out[565]=
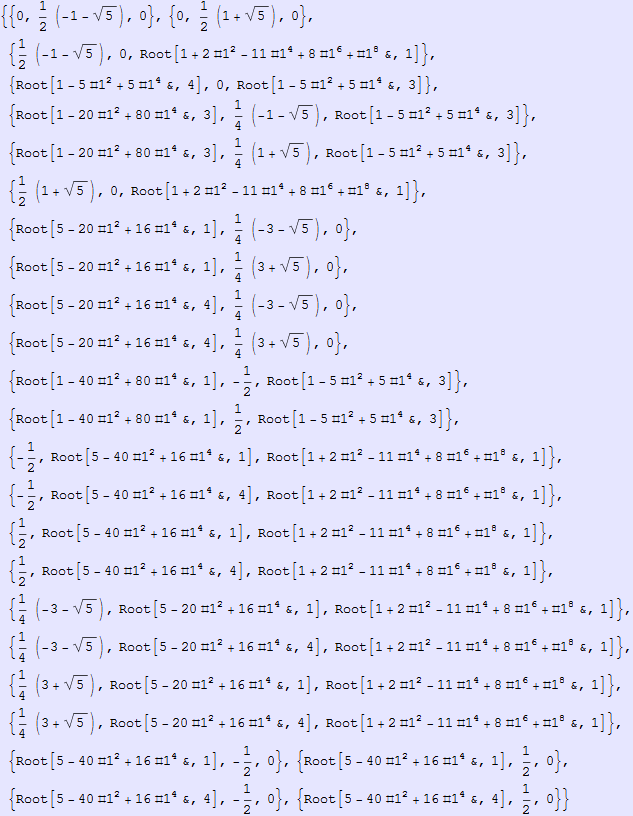
Johnson Polyhedra
Geometry