.
Elongated pentagonal orthobicupola
In[314]:=
![]()
Out[314]=
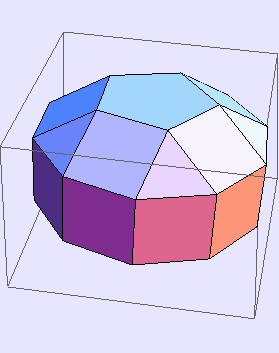
In[315]:=
![]()
Out[315]=
![]()
In[316]:=
![]()
Out[316]=
![]()
In[317]:=
![]()
Out[317]=
![]()
In[318]:=
![]()
Out[318]=
![]()
In[319]:=
![]()
Out[319]=
In[320]:=
![]()
Out[320]=
In[321]:=
![]()
Out[321]=
![]()
In[322]:=
![]()
Out[322]//InputForm=
Graphics3D[GraphicsComplex[{{0, (-1 - Sqrt[5])/2, -1/2}, {0, (-1 - Sqrt[5])/2, 1/2},
{0, (1 + Sqrt[5])/2, -1/2}, {0, (1 + Sqrt[5])/2, 1/2}, {Sqrt[1/2 + 1/(2*Sqrt[5])], 0,
(-5 - Sqrt[10*(5 - Sqrt[5])])/10}, {Sqrt[1/2 + 1/(2*Sqrt[5])], 0, (5 + Sqrt[10*(5 - Sqrt[5])])/10},
{Sqrt[(5 - Sqrt[5])/10]/2, (-1 - Sqrt[5])/4, (-5 - Sqrt[10*(5 - Sqrt[5])])/10},
{Sqrt[(5 - Sqrt[5])/10]/2, (-1 - Sqrt[5])/4, (5 + Sqrt[10*(5 - Sqrt[5])])/10},
{Sqrt[(5 - Sqrt[5])/10]/2, (1 + Sqrt[5])/4, (-5 - Sqrt[10*(5 - Sqrt[5])])/10},
{Sqrt[(5 - Sqrt[5])/10]/2, (1 + Sqrt[5])/4, (5 + Sqrt[10*(5 - Sqrt[5])])/10},
{-Sqrt[5/8 + Sqrt[5]/8], (-3 - Sqrt[5])/4, -1/2}, {-Sqrt[5/8 + Sqrt[5]/8], (-3 - Sqrt[5])/4, 1/2},
{-Sqrt[5/8 + Sqrt[5]/8], (3 + Sqrt[5])/4, -1/2}, {-Sqrt[5/8 + Sqrt[5]/8], (3 + Sqrt[5])/4, 1/2},
{Sqrt[5/8 + Sqrt[5]/8], (-3 - Sqrt[5])/4, -1/2}, {Sqrt[5/8 + Sqrt[5]/8], (-3 - Sqrt[5])/4, 1/2},
{Sqrt[5/8 + Sqrt[5]/8], (3 + Sqrt[5])/4, -1/2}, {Sqrt[5/8 + Sqrt[5]/8], (3 + Sqrt[5])/4, 1/2},
{-Sqrt[1/4 + 1/(2*Sqrt[5])], -1/2, (-5 - Sqrt[10*(5 - Sqrt[5])])/10},
{-Sqrt[1/4 + 1/(2*Sqrt[5])], -1/2, (5 + Sqrt[10*(5 - Sqrt[5])])/10},
{-Sqrt[1/4 + 1/(2*Sqrt[5])], 1/2, (-5 - Sqrt[10*(5 - Sqrt[5])])/10},
{-Sqrt[1/4 + 1/(2*Sqrt[5])], 1/2, (5 + Sqrt[10*(5 - Sqrt[5])])/10}, {-Sqrt[5/4 + Sqrt[5]/2], -1/2, -1/2},
{-Sqrt[5/4 + Sqrt[5]/2], -1/2, 1/2}, {-Sqrt[5/4 + Sqrt[5]/2], 1/2, -1/2},
{-Sqrt[5/4 + Sqrt[5]/2], 1/2, 1/2}, {Sqrt[5/4 + Sqrt[5]/2], -1/2, -1/2},
{Sqrt[5/4 + Sqrt[5]/2], -1/2, 1/2}, {Sqrt[5/4 + Sqrt[5]/2], 1/2, -1/2},
{Sqrt[5/4 + Sqrt[5]/2], 1/2, 1/2}}, Polygon[{{22, 10, 4, 14}, {20, 22, 26, 24}, {8, 20, 12, 2},
{6, 8, 16, 28}, {10, 6, 30, 18}, {18, 4, 10}, {14, 26, 22}, {24, 12, 20}, {2, 16, 8}, {28, 30, 6},
{10, 22, 20, 8, 6}, {13, 3, 9, 21}, {23, 25, 21, 19}, {1, 11, 19, 7}, {27, 15, 7, 5}, {17, 29, 5, 9},
{9, 3, 17}, {21, 25, 13}, {19, 11, 23}, {7, 15, 1}, {5, 29, 27}, {5, 7, 19, 21, 9}, {17, 3, 4, 18},
{3, 13, 14, 4}, {13, 25, 26, 14}, {25, 23, 24, 26}, {23, 11, 12, 24}, {11, 1, 2, 12}, {1, 15, 16, 2},
{15, 27, 28, 16}, {27, 29, 30, 28}, {29, 17, 18, 30}}]]]
In[323]:=
![]()
Out[323]=
![]()
In[324]:=
![]()
Out[324]=
![]()
In[325]:=
![]()
Out[325]=
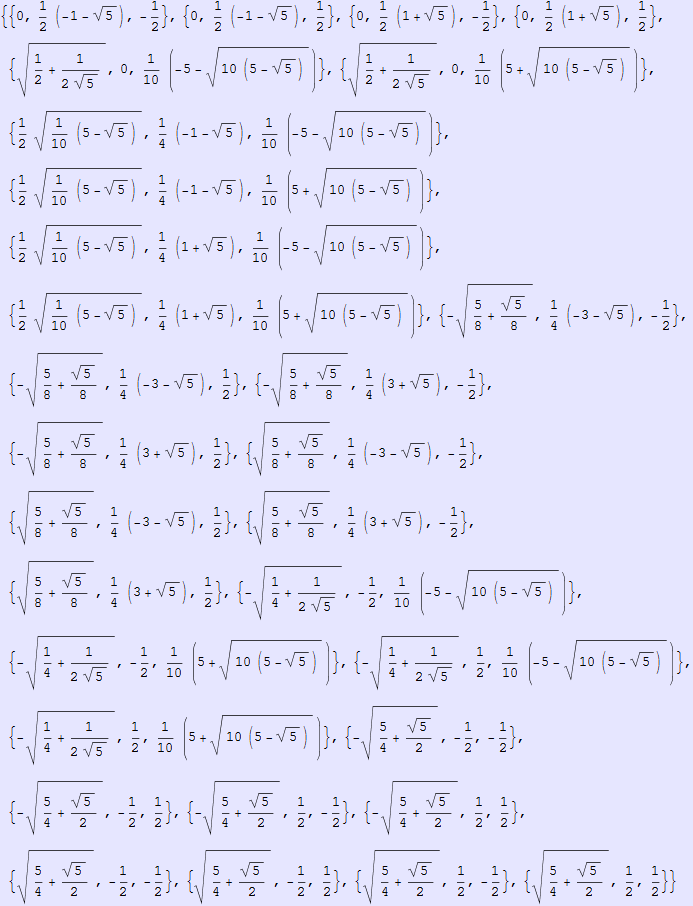
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

