Witch of Agnesi

In mathematics, the witch of Agnesi, sometimes called the witch of Maria Agnesi (named for Maria Agnesi) is the curve defined as follows.

Equations

Suppose the point O is the origin, and that M is on the positive y-axis. Suppose the radius of the circle is a.

Then the curve has Cartesian equation y .

Note that if a=1/2, then this equation becomes the very simple .

Parametrically, if is the angle between OM and OA, measured clockwise, then the curve is defined by the equations

Another parametrization, with being the angle between OA and the x-axis, increasing anti-clockwise is

Examples

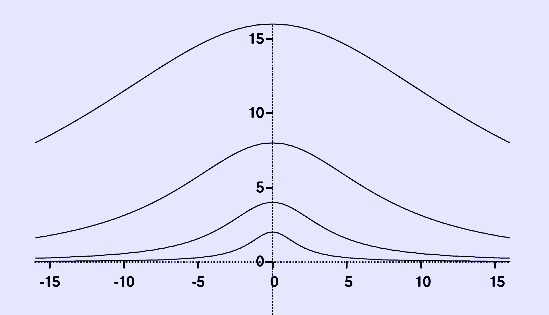
The figure to the right shows examples of this curve for a=1, a=2, a=4, and a=8.

Properties

The area between the Witch and its asymptote is four times the area of the fixed circle (i.e., 4πa²).

The volume of revolution of the Witch, about its asymptote, is 4π²a³.

The centroid of the curve is at .

History

The curve was studied by Fermat, Guido Grandi in 1701, and by Maria Agnesi in 1748.

In Italian, this curve is called la versiera di Agnesi which means "the curve of Agnesi". This was once interpreted by a Cambridge professor, John Colson, to mean "l'avversiera di Agnesi" where "avversiera" means "witch", and the mistranslation stuck as mentioned in "Fermat's Enigma" by Simon Singh.

See also

* Cauchy distribution

Links

* "The Witch of Agnesi". John H. Lienhard. The Engines of Our Ingenuity. NPR. KUHF-FM Houston. 2002. No. 1741. Transcript.

* Weisstein, Eric W.. Witch of Agnesi. MathWorld. A Wolfram Web Resource.

* MacTutor biography of Agnesi.