Catalan's constant

In mathematics, Catalan's constant G, which occasionally appears in estimates in combinatorics, is defined by

where β is the Dirichlet beta function. Its numerical value [1] is approximately (sequence A006752 in OEIS)

G = 0.915 965 594 177 219 015 054 603 514 932 384 110 774 …

It is not known whether G is rational or irrational.

Catalan's constant was named after Eugène Charles Catalan.

Integral identities

Some identities include

along with

where K(x) is a complete elliptic integral of the first kind, and

Uses

G appears in combinatorics, as well as in values of the second polygamma function, also called the trigamma function, at fractional arguments:

Simon Plouffe gives an infinite collection of identities between the trigamma function, π2 and Catalan's constant; these are expressible as paths on a graph.

It also appears in connection with the hyperbolic secant distribution.

Quickly converging series

The following two formulas involve quickly converging series, and are thus appropriate for numerical computation:

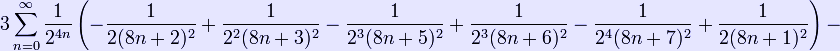
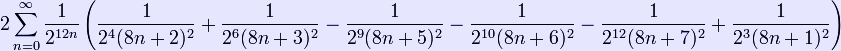
and

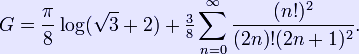
The theoretical foundations for such series is given by Broadhurst.[1]

Known digits

The number of known digits of Catalan's constant G has increased dramatically during the last decades. This is due both to the increase of performance of computers as well as to algorithmic improvements.[2]
Number of known decimal digits of Catalan's constant G Date Decimal digits Computation performed by
1865 14 Eugène Charles Catalan
1877 20 James W. L. Glaisher
1913 32 James W. L. Glaisher
1990 20,000 Greg J. Fee
1996 50,000 Greg J. Fee
August 14, 1996 100,000 Greg J. Fee & Simon Plouffe
September 29, 1996 300,000 Thomas Papanikolaou
1996 1,500,000 Thomas Papanikolaou
1997 3,379,957 Patrick Demichel
January 4, 1998 12,500,000 Xavier Gourdon
2001 100,000,500 Xavier Gourdon & Pascal Sebah
2002 201,000,000 Xavier Gourdon & Pascal Sebah
October 2006 5,000,000,000 Shigeru Kondo & Steve Pagliarulo[3]
August 2008 10,000,000,000 Shigeru Kondo & Steve Pagliarulo[4]
January 31, 2009 15,510,000,000 Alexander J. Yee & Raymond Chan[5]
April 16, 2009 31,026,000,000 Alexander J. Yee & Raymond Chan[5]

See also

* Zeta constant

Notes

1. ^ D.J. Broadhurst, "Polylogarithmic ladders, hypergeometric series and the ten millionth digits of ζ(3) and ζ(5)", (1998) arXiv math.CA/9803067
2. ^ Gourdon, X., Sebah, P; Constants and Records of Computation
3. ^ Shigeru Kondo's website
4. ^ Constants and Records of Computation
5. ^ a b Large Computations

References

* Victor Adamchik, 33 representations for Catalan's constant (undated)
* Adamchik,, Victor (2002). "A certain series associated with Catalan's constant". Zeitschr. f. Analysis und ihre Anwendungen (ZAA) 21 (3): 1–10. MR1929434. http://www-2.cs.cmu.edu/~adamchik/articles/csum.html.
* Simon Plouffe, A few identities (III) with Catalan, (1993) (Provides over one hundred different identities).
* Simon Plouffe, A few identities with Catalan constant and Pi^2, (1999) (Provides a graphical interpretation of the relations)
* Weisstein, Eric W., "Catalan's Constant" from MathWorld.
* Catalan constant: Generalized power series at the Wolfram Functions Site
* Greg Fee, Catalan's Constant (Ramanujan's Formula) (1996) (Provides the first 300,000 digits of Catalan's constant.).
* Bradley, David M. (1999). "A class of series acceleration formulae for Catalan's constant". The Ramanujan Journal 3 (2): 159–173. doi:10.1023/A:1006945407723. MR1703281.
* Bradley, David M. (2007). "A class of series acceleration formulae for Catalan's constant". arΧiv:0706.0356.
* Bradley, David M. (2001), Representations of Catalan's constant

Mathematical Constants