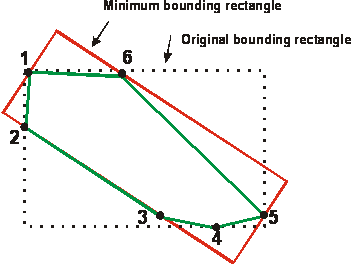
Minimum bounding rectangle of a polygon The axis-aligned minimum bounding box (MBB, AAMBB, AABB) for a set S in the N-dimensional space endowed with a coordinate system is the box or hyperrectangle of minimal dimensions with its edges parallel to the coordinate axes that contains S. More formally, the MBB is the Cartesian product of N intervals each of which is defined by the minimal and maximal value of the corresponding coordinate for the points in S. In many contexts the qualifiers "axis-aligned" and even "minimum" may be omitted. On the other hand, the term oriented MBB is used for minimum bounding boxes that have an orientation other than parallel to the coordinate axes. The term "box"/"hyperrectangle" comes from its usage in the Cartesian coordinate system, where it is indeed visualized as a rectangle (two-dimensional case), rectangular parallelepiped (three-dimensional case), etc. In the two-dimensional case it is called minimum bounding rectangle. Minimal bounding boxes are used to an approximate location of an object in question and as a very simple descriptor of its shape. For example, in computational geometry and its applications when it is required to find intersections in the set of objects, the initial check is the intersections between their MBBs. Since it is usually a much less expensive operation than the check of the actual intersection (because it only requires comparisons of coordinates), it allows to quickly exclude from checks the pairs that are far apart.
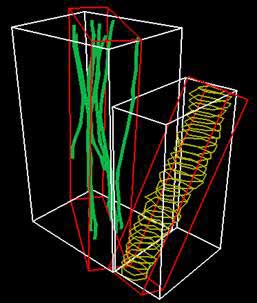
Two three-dimensional Minimum bounding box of 2 objects In digital image processing, the bounding box is merely the coordinates of the rectangular border that fully encloses a digital image when it is placed over a page, a canvas, a screen or other similar bidimensional background. See also * Bounding volume Retrieved from "http://en.wikipedia.org/"
|
|