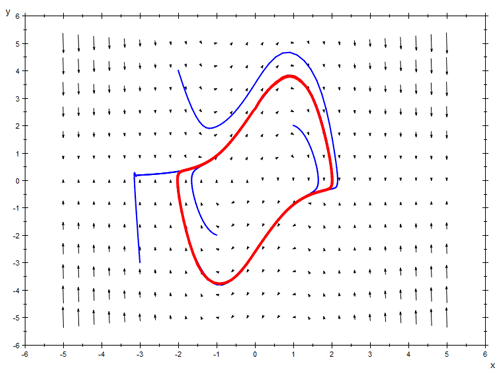
Phase portrait of the unforced Van der Pol oscillator, showing a limit cycle and the direction field. (*) n dynamics, the Van der Pol oscillator (named for Dutch physicist Balthasar van der Pol) is a type of nonconservative oscillator with nonlinear damping. It evolves in time according to the second order differential equation: where x is the position coordinate — which is a function of the time t, and μ is a scalar parameter indicating the strength of the nonlinear damping. It can be proven via Liénard's Theorem that there exists a limit cycle for the undriven Van der Pol oscillator, thus making it an example of a Liénard system. History The van der Pol oscillator was originally “discovered” by the Dutch electrical engineer and physicist Balthasar van der Pol. Van der Pol found stable oscillations, now known as limit cycles, in electrical circuits employing vacuum tubes. When these circuits are driven near the limit cycle they become entrained, i.e. the driving signal pulls the current along with it. Van der Pol and his colleague van der Mark reported in the September 1927 issue of Nature [1] that at certain drive frequencies an irregular noise was heard. This irregular noise was always heard near the natural entrainment frequencies. This was one of the first discovered instances of deterministic chaos. The van der Pol equation has a long history of being used in both the physical and biological sciences. For instance, in biology, Fitzhugh[2] and Nagumo[3] extended the equation in a planar field as a model for action potentials of neurons. The equation has also been utilised in seismology to model the two plates in a geological fault. Results * When μ < 0, the system will be damped. * When μ = 0, i.e. there is no damping function, the equation becomes: This is a form of the simple harmonic oscillator. Therefore, x is always varying with t at a proportional rate to { * When μ ≥ 0, the system will enter a limit cycle, where energy continues to be conserved. Energy can still be lost and work done if the system does not enter a limit cycle immediately. * When |μ| >> 0, the system is heavily damped and loses all energy extremely quickly. The Forced Van der Pol oscillator The forced, or driven, van der Pol oscillator takes the 'original' function and adds a driving function Asin(ωt) to give a differential equation of the form: where A is the amplitude, or displacement of the wave function and ω is its angular velocity. References 1. ^ van der Pol, B. and van der Mark, J., “Frequency demultiplication”, Nature, 120, 363-364, (1927). 2. ^ Fitzhugh, R., “Impulses and physiological in theoretical models of nerve membranes”, Biophysics J, 1, 445-466, (1961). 3. ^ Nagumo, J., S. Arimoto, and S. Yoshizawa, "An active pulse transmission line simulating nerve axon", Proc IRE, 50, 2061-2070, (1962). Links Retrieved from "http://en.wikipedia.org/"
|
|
0
}, the velocity, i.e. the distance of the pendulum, say, from the zero point, is proportional to its velocity from that same point. Due to this energy is conserved and there is no work done.
