Stochastic tunneling (STUN) is an approach to global optimization based on the Monte Carlo method-sampling of the function to be minimized. Idea
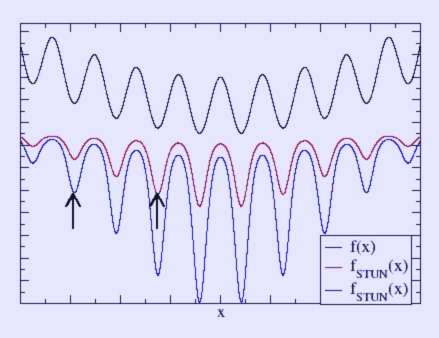
Schematic one-dimensional test function (black) and STUN effective potential (red & blue), where the minimum indicated by the arrows is the best minimum found so far. All wells that lie above the best minimum found are suppressed. If the dynamical process can escape the well around the current minimum estimate it will not be trapped by other local minima that are higher. Wells with deeper minima are enhanced. The dynamical process is accelerated by that. (*) Monte Carlo method-based optimization techniques sample the objective function by randomly "hopping" from the current solution vector to another with a difference in the function value of ΔE. The acceptance probability of such a trial jump is in most cases chosen to be The general idea of STUN is to circumvent the slow dynamics of ill-shaped energy functions that one encounters for example in spin glasses by tunneling through such barriers. This goal is achieved by Monte Carlo sampling of a transformed function that lacks this slow dynamics. In the "standard-form" the transformation reads The effect of such a transformation is shown in the graph. Other approaches * Simulated annealing References * K. Hamacher (2006). "Adaptation in Stochastic Tunneling Global Optimization of Complex Potential Energy Landscapes". Europhys. Lett. 74 (6): 944. Retrieved from "http://en.wikipedia.org/"
 |
|
||||||||||||
(Metropolis criterion) with an appropriate parameter β.
where fo is the lowest function value found so far. This transformation preserves the loci of the minima.